
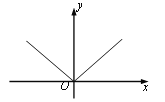
【题目】数学概念:百度百科上这样定义绝对值函数:y=│x│=![]()
并给出了函数的图像(如图).
方法迁移
借鉴研究正比例函数y=kx与一次函数y=kx+b(k,b是常数,且k≠0)之间关系的经验,我们来研究函数y=│x+a│(a是常数)的图像与性质.
“从‘1’开始”
我们尝试从特殊到一般,先研究当a=1时的函数y=│x+1│.
按照要求完成下列问题:
(1)观察该函数表达式,直接写出y的取值范围;
(2)通过列表、描点、画图,在平面直角坐标系中画出该函数的图像.
“从‘1’到一切”
(3)继续研究当a的值为-2,-![]() ,2,3,…时函数y=│x+a│的图像与性质,
,2,3,…时函数y=│x+a│的图像与性质,
尝试总结:
①函数y=│x+a│(a≠0)的图像怎样由函数y=│x│的图像平移得到?
②写出函数y=│x+a│的一条性质.
知识应用
(4)已知A(x1,y1),B(x2,y2)是函数y=│x+a│的图像上的任意两点,且满足x1<x2≤-1时, y1>y2,则a的取值范围是 .
【答案】(1)y≥0.(2)见解析;(3)①见解析;②答案不唯一,如当x>-a时,y随x的增大而增大;当x<-a时,y随x的增大而减小.(4)a≤1.
【解析】
(1)根据绝对值的概念可以写出答案;
(2)通过列表、描点、连线,即可画出函数图象;
(3)当a的值为-2和3时,通过列表、描点、连线,画出函数图象,通过观察图象得出①、②的答案;
(4)通过观察图象:函数y=│x+a│的对称轴为直线![]() ,根据函数的增减性,可以求得a的取值范围.
,根据函数的增减性,可以求得a的取值范围.
(1)根据绝对值的性质得: y≥0.
(2)列表:
x |
| -4 | -3 | -2 | -1 | 0 | 1 | 2 |
|
y=│x+1│ |
| 3 | 2 | 1 | 0 | 1 | 2 | 3 |
|
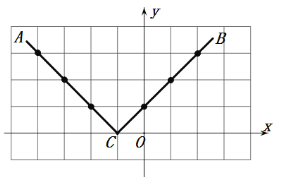
通过描点、连线,射线CA、CB就是所求作;
(3)当a的值为-2和3时,仿照(2)的方法在同一平面直角坐标系中画出函数的图像,如下图:
x |
| -1 | 2 | 5 |
|
y=│x-2│ |
| 3 | 0 | 3 |
|
x |
| -6 | -3 | 0 |
|
y=│x+3│ |
| 3 | 0 | 3 |
|
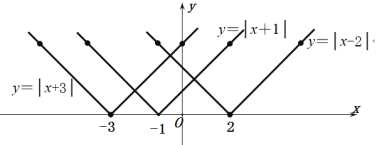
①函数y=│x+a│(a≠0)的图像是由函数y=│x│的图像向左(a>0)或向右(a<0)平移│a│个单位得到.
②答案不唯一,如:当x>-a时,y随x的增大而增大;当x<-a时,y随x的增大而减小.
(4)通过观察函数的图象知:函数y=│x+a│的对称轴为直线![]() ,
,
根据题意:满足x1<x2≤-1时, y1>y2,属于减函数,是在对称轴![]() 的左侧,
的左侧,
所以-1≤-a,
所以![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
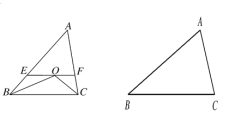
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过O做EF∥BC分别交AB、AC于E、F.
(1)求证:EF=BE+CF.
(2)在△ABC中,∠ABC的角平分线与∠ACB相邻的外角的平分线相交于点O,过O做EF∥BC分别交AB、AC于E、F,请你画出图形(不要求尺规作图),并直接写出EF、BE、CF之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解答问题.
(阅读)例题:求多项式m2 + 2mn+2n2-6n+13的最小值.
解;m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4,
∵(m+n)2![]() 0, (n-3)2
0, (n-3)2![]() 0
0
∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是
(2)己知a、b、c是△ABC的三边,且满足a2+b2=l0a+8b-41,求第三边c的取值范围;
(3)求多项式-2x2+4xy-3y2 -3y2-6y+7 的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
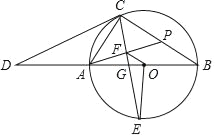
【题目】如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
(Ⅰ)求∠CPA的度数;
(Ⅱ)连接OF,若AC=![]() ,∠D=30°,求线段OF的长.
,∠D=30°,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
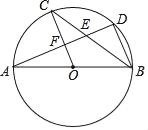
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD与BC,OC分别相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤△CEF≌△BED.其中一定成立的结论是_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
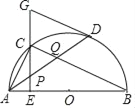
【题目】如图,AB是半圆O的直径,点D是半圆O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.
(1)求证:GP=GD;
(2)求证:P是线段AQ的中点;
(3)连接CD,若CD=2,BC=4,求⊙O的半径和CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=AC=20 cm.动点P,Q分别从A,B两点同时出发,沿三角形的边匀速运动.已知点P,点Q的速度都是2 cm/s,当点P第一次到达B点时,P,Q两点同时停止运动.设点P的运动时间为t(s).
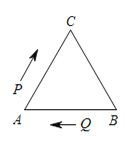
(1)∠A=______度;
(2)当0<t<10,且△APQ为直角三角形时,求t的值;
(3)当△APQ为等边三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的直径,
的直径,![]() ,
,![]() 、
、![]() 分别与圆相交于
分别与圆相交于![]() 、
、![]() ,那么下列等式中一定成立的是( )
,那么下列等式中一定成立的是( )
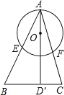
A. AEBF=AFCF B. AEAB=AOAD'
C. AEAB=AFAC D. AEAF=AOAD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com