
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过O做EF∥BC分别交AB、AC于E、F.
(1)求证:EF=BE+CF.
(2)在△ABC中,∠ABC的角平分线与∠ACB相邻的外角的平分线相交于点O,过O做EF∥BC分别交AB、AC于E、F,请你画出图形(不要求尺规作图),并直接写出EF、BE、CF之间的关系.
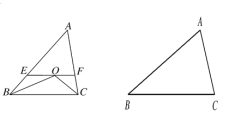
【答案】(1)证明见解析;(2)作图见解析;EF=BE-CF
【解析】
(1)根据角平分线和平行线的性质分别证明∠EBO=∠EOB,∠FOC=∠FCO,从而得出EO=BE,FO=CF,即可解决问题;
(2)根据角平分线的额作法步骤,分别作出∠ABC和∠ACB的角平分线,两条角平分线的交点即为点O,
(1)证明:∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠EOB=∠OBC,
∴∠EBO=∠EOB,
∴EO=BE,
同理:FO=CF,
∴EO+FO=BE+CF,
即EF=BE+CF.
(2)以点B为圆心,以任意长为半径作弧,分别交BA和BC与点M和点D;
分别以M和D为圆心,以大于MD的一半为半径作弧,交于点N,作射线BN,则射线BN即为∠ABC的角平分线;
同理作∠ACB外角的角平分线,两线交于点O,过点O作BC的平行线交AB与点E,交AC于点F.如图所示:
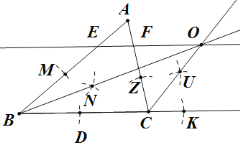
∵OE∥BC,
∴∠EOB=∠CBO,
∵BN是∠ABC的角平分线,
∴∠ABN=∠CBO,
∴∠ABN=∠EOB,
∴BE=OE,
∵OE∥BC,
∴∠OCK=∠FOC,
∵CU是∠ACK的角平分线,
∴∠OCK=∠FCO,
∴∠FCO=∠FOC,
∴FO=CF,
∴BE=EO=FO+EF=EF+CF,
∴EF=BE-CF


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.(1)甲蚂蚁选择“向左”爬行的概率为________;
(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梦想商店进了一批服装,进货单价为![]() 元,如果按每件
元,如果按每件![]() 元出售,可销售
元出售,可销售![]() 件,如果每件提价
件,如果每件提价![]() 元出售,其销售量就减少
元出售,其销售量就减少![]() 件.
件.
![]() 现在获利
现在获利![]() 元,且销售成本不超过
元,且销售成本不超过![]() 元,问这种服装销售单价应定多少元?这时应进多少服装?
元,问这种服装销售单价应定多少元?这时应进多少服装?
![]() 当销售单价应定多少元时,该商店获得最大利润?最大利润是多少元?
当销售单价应定多少元时,该商店获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC中,∠A=68°,以AB为直径的⊙O与AC,BC的交点分别为D,E
(Ⅰ)如图①,求∠CED的大小;
(Ⅱ)如图②,当DE=BE时,求∠C的大小.
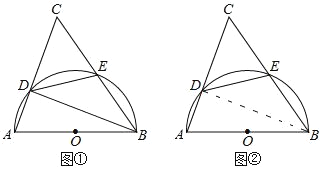
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinxcosy+cosxsiny.
据此判断下列等式成立的是 (写出所有正确的序号)
①cos(﹣60°)=﹣![]() ;
;
②sin75°=![]() ;
;
③sin2x=2sinxcosx;
④sin(x﹣y)=sinxcosy﹣cosxsiny.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校传统文化社团某天进行纳新活动,组织初一新生选报兴趣学社,由于当天报名人数较多,从现场随机抽查部分学生的报名意向进行统计,并绘制出不完全的频数分布表和频数分布直方图,如下所示:
传统文化 学社 | 报名频数 (人数) | 报名 频率 | 录取率 |
灯谜 | 12 |
|
|
书法 | 27 | 0.45 | 0.4 |
剪纸 |
| 0.3 |
|
南音 |
|
|
|
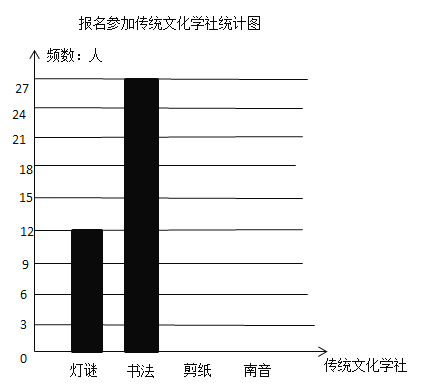
请根据上述图表,完成下列各题:
(1)填空:![]() ,
,![]() ,
,![]() ,现场共抽查了 名学生;
,现场共抽查了 名学生;
(2)请把条线统计图补充完整;
(3)现有1200个学生报名参加该校传统文化社团,则可以估计被剪纸学社录取的学生数比南音学社录取的学生数多了多少人?若把所有被录取人数按表中学社制作成扇形统计图,则被灯谜学社录取的学生数的扇形圆心角为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
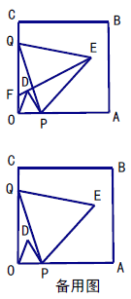
【题目】如图,正方形![]() 的边长为8,
的边长为8,![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() 为
为![]() 边上的一个动点,分别以
边上的一个动点,分别以![]() 为边在正方形
为边在正方形![]() 内部作等边三角形
内部作等边三角形![]() 和等边三角形
和等边三角形![]() .
.
(1)证明:![]() ;
;
(2)直线![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 在运动过程中.
在运动过程中.
①![]() 的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由;
的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由;
②连结![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
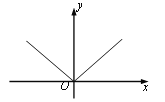
【题目】数学概念:百度百科上这样定义绝对值函数:y=│x│=![]()
并给出了函数的图像(如图).
方法迁移
借鉴研究正比例函数y=kx与一次函数y=kx+b(k,b是常数,且k≠0)之间关系的经验,我们来研究函数y=│x+a│(a是常数)的图像与性质.
“从‘1’开始”
我们尝试从特殊到一般,先研究当a=1时的函数y=│x+1│.
按照要求完成下列问题:
(1)观察该函数表达式,直接写出y的取值范围;
(2)通过列表、描点、画图,在平面直角坐标系中画出该函数的图像.
“从‘1’到一切”
(3)继续研究当a的值为-2,-![]() ,2,3,…时函数y=│x+a│的图像与性质,
,2,3,…时函数y=│x+a│的图像与性质,
尝试总结:
①函数y=│x+a│(a≠0)的图像怎样由函数y=│x│的图像平移得到?
②写出函数y=│x+a│的一条性质.
知识应用
(4)已知A(x1,y1),B(x2,y2)是函数y=│x+a│的图像上的任意两点,且满足x1<x2≤-1时, y1>y2,则a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com