
【题目】已知,△ABC中,∠A=68°,以AB为直径的⊙O与AC,BC的交点分别为D,E
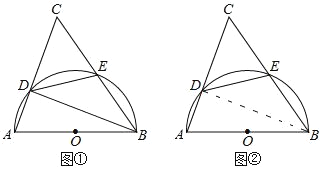
(Ⅰ)如图①,求∠CED的大小;
(Ⅱ)如图②,当DE=BE时,求∠C的大小.
【答案】(Ⅰ)68°(Ⅱ)56°
【解析】
(1)圆内接四边形的一个外角等于它的内对角,利用圆内接四边形的性质证明∠CED=∠A即可,(2)连接AE,在Rt△AEC中,先根据同圆中,相等的弦所对弧相等,再根据同圆中,相等的弧所对圆周角相等, 求出∠EAC,最后根据直径所对圆周是直角,利用直角三角形两锐角互余即可解决问题.
(Ⅰ)∵四边形ABED 圆内接四边形,
∴∠A+∠DEB=180°,
∵∠CED+∠DEB=180°,
∴∠CED=∠A,
∵∠A=68°,
∴∠CED=68°.
(Ⅱ)连接AE.
∵DE=BD,
∴![]() ,
,
∴∠DAE=∠EAB=![]() ∠CAB=34°,
∠CAB=34°,
∵AB是直径,
∴∠AEB=90°,
∴∠AEC=90°,
∴∠C=90°﹣∠DAE=90°﹣34°=56°


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() .
.
(1)求出点![]() ,点
,点![]() 的坐标.
的坐标.
(2)![]() 是直线
是直线![]() 上一动点,且
上一动点,且![]() 和
和![]() 的面积相等,求点
的面积相等,求点![]() 坐标.
坐标.
(3)如图2,平移直线![]() ,分别交
,分别交![]() 轴,
轴,![]() 轴于交于点
轴于交于点![]() ,
,![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,请直接写出所有符合条件的点
是等腰直角三角形?若存在,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
图1 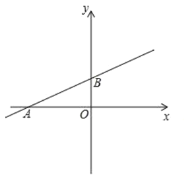 图2
图2 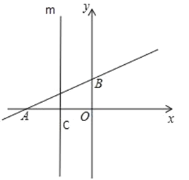
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他骑公共自行车比自驾车平均每小时少行驶45千米,他从家出发到上班地点,骑公共自行车所用的时间是自驾车所用的时间的4倍.小张骑公共自行车平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学计划为新生配备如图1所示的折叠椅.图2中的正方形ACBD是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.若正方形ACBD的面积为[9(2x-3y)2+12(2x-3y) (x+4y) +4(x+4y)2](米2)(x>y),你能求出这种折叠椅张开后的高度吗?
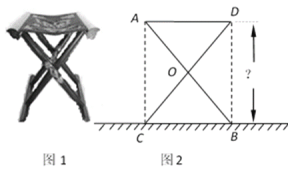
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
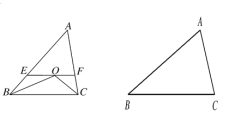
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过O做EF∥BC分别交AB、AC于E、F.
(1)求证:EF=BE+CF.
(2)在△ABC中,∠ABC的角平分线与∠ACB相邻的外角的平分线相交于点O,过O做EF∥BC分别交AB、AC于E、F,请你画出图形(不要求尺规作图),并直接写出EF、BE、CF之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=a ,AB=c,AC=b,则不能作为判定△ABC是直角三角形的条件的是( )
A.![]() B.∠A∶∠B∶∠C=1∶4∶3
B.∠A∶∠B∶∠C=1∶4∶3
C.a∶b∶c =7∶24∶25D.a∶b∶c =4∶5∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、点
、点![]() 同时出发,相向而行,速度都为
同时出发,相向而行,速度都为![]() .以
.以![]() 为一边向上作正方形
为一边向上作正方形![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() ,单位:
,单位:![]() ,正方形
,正方形![]() 和梯形
和梯形![]() 重合部分的面积为
重合部分的面积为![]() .
.
![]() 当
当![]() 时,点
时,点![]() 与点
与点![]() 重合.
重合.
![]() 当
当![]() 时,点
时,点![]() 在
在![]() 上.
上.
![]() 当点
当点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点)时,求
两点)时,求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
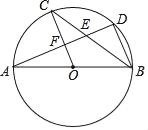
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD与BC,OC分别相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤△CEF≌△BED.其中一定成立的结论是_____.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com