
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、点
、点![]() 同时出发,相向而行,速度都为
同时出发,相向而行,速度都为![]() .以
.以![]() 为一边向上作正方形
为一边向上作正方形![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() ,单位:
,单位:![]() ,正方形
,正方形![]() 和梯形
和梯形![]() 重合部分的面积为
重合部分的面积为![]() .
.
![]() 当
当![]() 时,点
时,点![]() 与点
与点![]() 重合.
重合.
![]() 当
当![]() 时,点
时,点![]() 在
在![]() 上.
上.
![]() 当点
当点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点)时,求
两点)时,求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.

【答案】(1)1;(2)![]() ;(3)当点
;(3)当点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点)时,
两点)时,![]() 与
与![]() 之间的函数关系式为:
之间的函数关系式为: .
.
【解析】
(1)当点P与点Q重合时,此时AP=BQ=t,且AP+BQ=AB=2,由此列一元一次方程求出t的值;
(2)当点D在QF上时,如图1所示,此时AP=BQ=t.由相似三角形比例线段关系可得PQ=![]() t,从而由关系式AP+PQ+BQ=AB=2,列一元一次方程求出t的值;
t,从而由关系式AP+PQ+BQ=AB=2,列一元一次方程求出t的值;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,运动过程可以划分为两个阶段:
①当1<t≤![]() 时,如答图3所示,此时重合部分为梯形PDGQ.先计算梯形各边长,然后利用梯形面积公式求出S;
时,如答图3所示,此时重合部分为梯形PDGQ.先计算梯形各边长,然后利用梯形面积公式求出S;
②当![]() <t<2时,如答图4所示,此时重合部分为一个多边形.面积S由关系式“S=S正方形APDE﹣S△AQF﹣S△DMN”求出.
<t<2时,如答图4所示,此时重合部分为一个多边形.面积S由关系式“S=S正方形APDE﹣S△AQF﹣S△DMN”求出.
(1)当点P与点Q重合时,AP=BQ=t,且AP+BQ=AB=2,∴t+t=2,解得:t=1s.
故答案:1.
(2)当点D在QF上时,如图1所示,此时AP=BQ=t.
∵QF∥BC,APDE为正方形,∴△PQD∽△ABC,∴DP:PQ=AC:AB=2,则PQ=![]() DP=
DP=![]() AP=
AP=![]() t.
t.
由AP+PQ+BQ=AB=2,得:t+![]() t+t=2,解得:t=
t+t=2,解得:t=![]() .
.
故答案:![]() .
.
(3)当P、Q重合时,由(1)知,此时t=1;
当D点在BC上时,如答图2所示,此时AP=BQ=t,BP=![]() t,求得t=
t,求得t=![]() s,进一步分析可知此时点E与点F重合;
s,进一步分析可知此时点E与点F重合;
当点P到达B点时,此时t=2.
因此当P点在Q,B两点之间(不包括Q,B两点)时,其运动过程可分析如下:
①当1<t≤![]() 时,如答图3所示,此时重合部分为梯形PDGQ.
时,如答图3所示,此时重合部分为梯形PDGQ.
此时AP=BQ=t,∴AQ=2﹣t,PQ=AP﹣AQ=2t﹣2;
易知△ABC∽△AQF,可得AF=2AQ,EF=2EG,∴EF=AF﹣AE=2(2﹣t)﹣t=4﹣3t,EG=![]() EF=2﹣
EF=2﹣![]() t,∴DG=DE﹣EG=t﹣(2﹣
t,∴DG=DE﹣EG=t﹣(2﹣![]() t)=
t)=![]() t﹣2.
t﹣2.
S=S梯形PDGQ=![]() (PQ+DG)PD=
(PQ+DG)PD=![]() [(2t﹣2)+(
[(2t﹣2)+(![]() t﹣2)]t=
t﹣2)]t=![]() t2﹣2t;
t2﹣2t;
②当![]() <t<2时,如答图4所示,此时重合部分为一个多边形.
<t<2时,如答图4所示,此时重合部分为一个多边形.
此时AP=BQ=t,∴AQ=PB=2﹣t,易知△ABC∽△AQF∽△PBM∽△DNM,可得AF=2AQ,PM=2
又∵DM=DP﹣PM=t﹣(4﹣2t)=3t﹣4,∴DN=![]() (3t﹣4)=
(3t﹣4)=![]() t﹣2,DM=3t﹣4.
t﹣2,DM=3t﹣4.
S=S正方形APDE﹣S△AQF﹣S△DMN=AP2﹣![]() AQAF﹣
AQAF﹣![]() DNDM
DNDM
=t2﹣![]() (2﹣t)(4﹣2t)﹣
(2﹣t)(4﹣2t)﹣![]() ×
×![]() (3t﹣4)×(3t﹣4)
(3t﹣4)×(3t﹣4)
=﹣![]() t2+10t﹣8.
t2+10t﹣8.
综上所述:当点P在Q,B两点之间(不包括Q,B两点)时,S与t之间的函数关系式为:S= .
.


科目:初中数学 来源: 题型:
【题目】某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5 000个“单次营运里程”数据,这些里程数据均不超过25(公里),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.
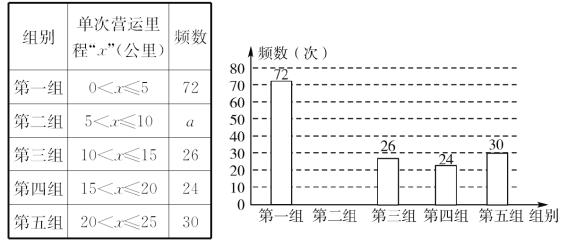
根据统计表、图提供的信息,解答下面的问题:
(1)表中a=________;样本中“单次营运里程”不超过15公里的频率为________;(2)请把频数分布直方图补充完整;
(3)请估计该公司这5 000个“单次营运里程”超过20公里的次数;
查看答案和解析>>
科目:初中数学 来源: 题型:
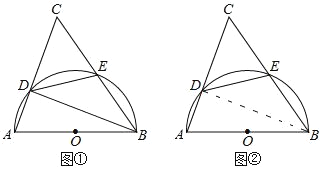
【题目】已知,△ABC中,∠A=68°,以AB为直径的⊙O与AC,BC的交点分别为D,E
(Ⅰ)如图①,求∠CED的大小;
(Ⅱ)如图②,当DE=BE时,求∠C的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校传统文化社团某天进行纳新活动,组织初一新生选报兴趣学社,由于当天报名人数较多,从现场随机抽查部分学生的报名意向进行统计,并绘制出不完全的频数分布表和频数分布直方图,如下所示:
传统文化 学社 | 报名频数 (人数) | 报名 频率 | 录取率 |
灯谜 | 12 |
|
|
书法 | 27 | 0.45 | 0.4 |
剪纸 |
| 0.3 |
|
南音 |
|
|
|
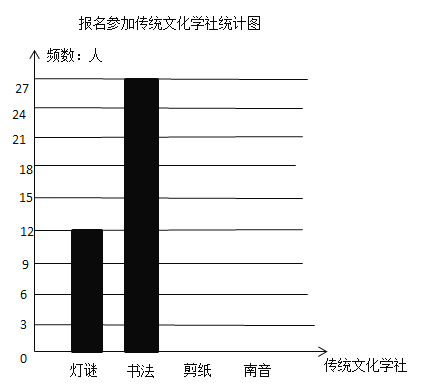
请根据上述图表,完成下列各题:
(1)填空:![]() ,
,![]() ,
,![]() ,现场共抽查了 名学生;
,现场共抽查了 名学生;
(2)请把条线统计图补充完整;
(3)现有1200个学生报名参加该校传统文化社团,则可以估计被剪纸学社录取的学生数比南音学社录取的学生数多了多少人?若把所有被录取人数按表中学社制作成扇形统计图,则被灯谜学社录取的学生数的扇形圆心角为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,a,b分别是∠A,∠B的对边,c为斜边,如果已知两个元素a,∠B,就可以求出其余三个未知元素b,c,∠A.

(1)求解的方法有多种,请你按照下列步骤,完成一种求解过程.
第一步:已知:a,∠B,用关系式:_______________,求出:________________;
第二步:已知:_____,用关系式:_______________,求出:_________________;
第三步:已知:_____,用关系式:_______________,求出:_________________.
(2)请你分别给出a,∠B的一个具体数据,然后按照(1)中的思路,求出b,c,∠A的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
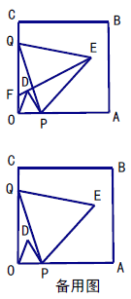
【题目】如图,正方形![]() 的边长为8,
的边长为8,![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() 为
为![]() 边上的一个动点,分别以
边上的一个动点,分别以![]() 为边在正方形
为边在正方形![]() 内部作等边三角形
内部作等边三角形![]() 和等边三角形
和等边三角形![]() .
.
(1)证明:![]() ;
;
(2)直线![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 在运动过程中.
在运动过程中.
①![]() 的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由;
的度数是否发生改变?若不变,求出这个角的度数;若改变,说明理由;
②连结![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,![]() 是直线
是直线![]() 上一动点,
上一动点,![]() 两点在直线
两点在直线![]() 的同侧,且点
的同侧,且点![]() 所在直线与
所在直线与![]() 不平行.
不平行.

(1)当![]() 点运动到
点运动到![]() 位置时,距离
位置时,距离![]() 点最近,在图1中的直线
点最近,在图1中的直线![]() 上画出点
上画出点![]() 的位置;
的位置;
(2)当![]() 点运动到
点运动到![]() 位置时,与
位置时,与![]() 点的距离和与
点的距离和与![]() 点距两相等,请在图2中作出
点距两相等,请在图2中作出![]() 位置;
位置;
(3)在直线![]() 上是否存在这样一点
上是否存在这样一点![]() ,使得到
,使得到![]() 点的距离与到
点的距离与到![]() 点的距离之和最小?若存在请在图3中作出这点,若不存在清说明理由.
点的距离之和最小?若存在请在图3中作出这点,若不存在清说明理由.
(要求:不写作法,请保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
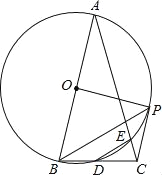
【题目】如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校甲、乙两名同学去爱国主义教育基地参观,该基地与学校相距2400米.甲从学校步行去基地,出发5分钟后乙再出发,乙从学校骑自行车到基地. 乙骑行到一半时,发现有东西忘带,立即返回,拿好东西之后再从学校出发.在骑行过程中,乙的速度保持不变,最后甲、乙两人同时到达基地. 已知,乙骑行的总时间是甲步行时间的![]() .设甲步行的时间为
.设甲步行的时间为![]() (分),图中线段OA表示甲离开学校的路程
(分),图中线段OA表示甲离开学校的路程![]() (米)与
(米)与![]() (分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程
(分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程![]() (米)与
(米)与![]() (分)的函数关系的图像.根据图中所给的信息,解答下列问题:
(分)的函数关系的图像.根据图中所给的信息,解答下列问题:
(1)甲步行的速度和乙骑行的速度;
(2)甲出发多少时间后,甲、乙两人第二次相遇?
(3)若![]() (米)表示甲、乙两人之间的距离,当
(米)表示甲、乙两人之间的距离,当![]() 时,求
时,求![]() (米)关于
(米)关于![]() (分)的函数关系式.
(分)的函数关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com