
【题目】某校传统文化社团某天进行纳新活动,组织初一新生选报兴趣学社,由于当天报名人数较多,从现场随机抽查部分学生的报名意向进行统计,并绘制出不完全的频数分布表和频数分布直方图,如下所示:
传统文化 学社 | 报名频数 (人数) | 报名 频率 | 录取率 |
灯谜 | 12 |
|
|
书法 | 27 | 0.45 | 0.4 |
剪纸 |
| 0.3 |
|
南音 |
|
|
|
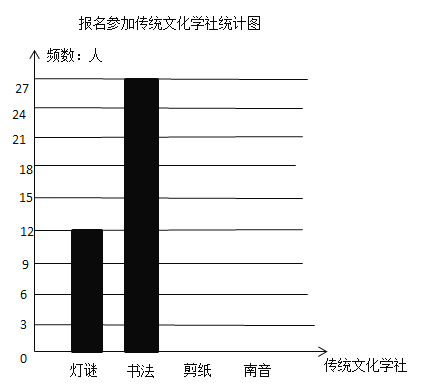
请根据上述图表,完成下列各题:
(1)填空:![]() ,
,![]() ,
,![]() ,现场共抽查了 名学生;
,现场共抽查了 名学生;
(2)请把条线统计图补充完整;
(3)现有1200个学生报名参加该校传统文化社团,则可以估计被剪纸学社录取的学生数比南音学社录取的学生数多了多少人?若把所有被录取人数按表中学社制作成扇形统计图,则被灯谜学社录取的学生数的扇形圆心角为多少度?
【答案】(1)18;3;0.25;60;(2)答案见解析;(3)168人;33.75°
【解析】
(1)根据书法人数和频率利用频数:总数=频率的公式求总数,然后分别求p,m,n,t,从而使问题得解;(2)根据m,n补充统计图;(3)用录取人数=总人数×频率×录取率分别计算,然后求出被剪纸学社录取的学生数比南音学社录取的学生数多了多少人,求出所有被录取人数,利用360°乘灯谜社录取人数在所有被录取人数中所占的百分比,求圆心角度数.
解:(1)根据题意可知:抽查学生总是为![]() 人
人
∴m=60×0.3=18
n=60-12-27-18=3
t=![]()
p=![]()
∴p+t =0.25
故答案为:18;3;0.25;60
(2)如图:
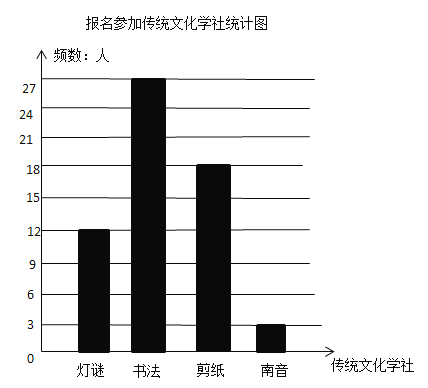
(3)剪纸学社录取率为p+t+0.35=0.6
∴剪纸录取学生1200×0.3×0.6=216人
南音学社录取率为t+0.75=0.8
∴南音学生录取学生1200×0.05×0.8=48人
∴被剪纸学社录取的学生数比南音学社录取的学生数多216-48=168人
书法社被录取1200×0.45×0.4=216人
灯谜社被录取1200×0.2×0.25=60人
所以共录取216+48+216+60=640人
被灯谜学社录取的学生数的扇形圆心角为![]()


科目:初中数学 来源: 题型:
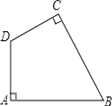
【题目】如图,在四边形ABCD中,∠A=∠C=90°.
(1)用直尺和圆规作⊙O,使它经过A、B、D三点(保留作图痕迹);
(2)点C是否在⊙O上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学计划为新生配备如图1所示的折叠椅.图2中的正方形ACBD是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.若正方形ACBD的面积为[9(2x-3y)2+12(2x-3y) (x+4y) +4(x+4y)2](米2)(x>y),你能求出这种折叠椅张开后的高度吗?
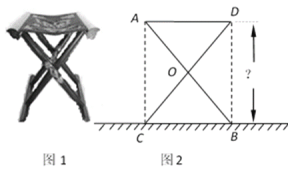
查看答案和解析>>
科目:初中数学 来源: 题型:
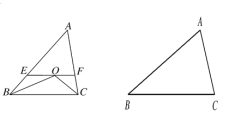
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过O做EF∥BC分别交AB、AC于E、F.
(1)求证:EF=BE+CF.
(2)在△ABC中,∠ABC的角平分线与∠ACB相邻的外角的平分线相交于点O,过O做EF∥BC分别交AB、AC于E、F,请你画出图形(不要求尺规作图),并直接写出EF、BE、CF之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=a ,AB=c,AC=b,则不能作为判定△ABC是直角三角形的条件的是( )
A.![]() B.∠A∶∠B∶∠C=1∶4∶3
B.∠A∶∠B∶∠C=1∶4∶3
C.a∶b∶c =7∶24∶25D.a∶b∶c =4∶5∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:在小学已经学过“正方形的四条边都相等,正方形的四个内角都是直角”,试利用上述知识,并结合已学过的知识解答下列问题:
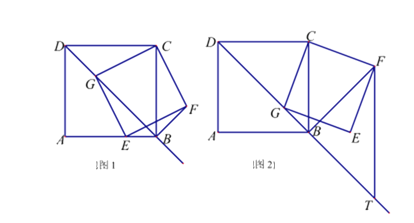
如图1,在正方形ABCD中,G是射线DB上的一个动点(点G不与点D重合),以CG为边向下作正方形CGEF.
(1)当点G在线段BD上时,求证:![]() ;
;
(2)连接BF,试探索:BF,BG与AB的数量关系,并说明理由;
(3)若AB=a(a是常数),如图2,过点F作FT∥BC,交射线DB于点T,问在点G的运动过程中,GT的长度是否会随着G点的移动而变化?若不变,请求出GT的长度;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、点
、点![]() 同时出发,相向而行,速度都为
同时出发,相向而行,速度都为![]() .以
.以![]() 为一边向上作正方形
为一边向上作正方形![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() ,单位:
,单位:![]() ,正方形
,正方形![]() 和梯形
和梯形![]() 重合部分的面积为
重合部分的面积为![]() .
.
![]() 当
当![]() 时,点
时,点![]() 与点
与点![]() 重合.
重合.
![]() 当
当![]() 时,点
时,点![]() 在
在![]() 上.
上.
![]() 当点
当点![]() 在
在![]() ,
,![]() 两点之间(不包括
两点之间(不包括![]() ,
,![]() 两点)时,求
两点)时,求![]() 与
与![]() 之间的函数表达式.
之间的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解答问题.
(阅读)例题:求多项式m2 + 2mn+2n2-6n+13的最小值.
解;m2+2mn+2n2-6n+ 13= (m2 +2mn+n2)+ (n2-6n+9)+4= (m+n)2+(n-3)2+4,
∵(m+n)2![]() 0, (n-3)2
0, (n-3)2![]() 0
0
∴多项式m2+2mn+2n2-6n+ 13的最小值是4.
(解答问题)
(1)请写出例题解答过程中因式分解运用的公式是
(2)己知a、b、c是△ABC的三边,且满足a2+b2=l0a+8b-41,求第三边c的取值范围;
(3)求多项式-2x2+4xy-3y2 -3y2-6y+7 的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=AC=20 cm.动点P,Q分别从A,B两点同时出发,沿三角形的边匀速运动.已知点P,点Q的速度都是2 cm/s,当点P第一次到达B点时,P,Q两点同时停止运动.设点P的运动时间为t(s).
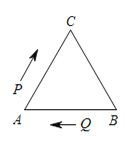
(1)∠A=______度;
(2)当0<t<10,且△APQ为直角三角形时,求t的值;
(3)当△APQ为等边三角形时,直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com