
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() .
.
(1)求出点![]() ,点
,点![]() 的坐标.
的坐标.
(2)![]() 是直线
是直线![]() 上一动点,且
上一动点,且![]() 和
和![]() 的面积相等,求点
的面积相等,求点![]() 坐标.
坐标.
(3)如图2,平移直线![]() ,分别交
,分别交![]() 轴,
轴,![]() 轴于交于点
轴于交于点![]() ,
,![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 是等腰直角三角形?若存在,请直接写出所有符合条件的点
是等腰直角三角形?若存在,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
图1 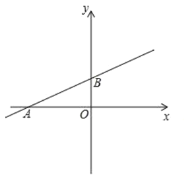 图2
图2 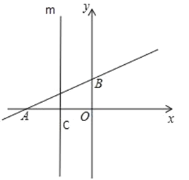
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]()
![]() .
.
【解析】
(1)根据A,B坐标的特点即可求解;
(2)分P点在线段AB上、直线AB上根据三角形的面积公式即可求解;
(3)设Q(-2,t),分别求出AB2,AQ2,BQ2,根据等腰三角形的性质分情况讨论即可求解.
(1)令y=![]() =0,解得x=-4,
=0,解得x=-4,
∴A(-4,0)
令x=0,y=![]() =2,
=2,
∴B(0,2)
(2)如图,当P点在线段AB上,设P(x,![]() )
)
∵![]() ,A(-4,0),B(0,2)
,A(-4,0),B(0,2)
∴CO=2=OB,OA=4
∵![]() 和
和![]() 的面积相等
的面积相等
∴![]() BO×(-x)=
BO×(-x)= ![]() CO×(
CO×(![]() ),即
),即![]() ×2×(-x)=
×2×(-x)= ![]() ×2×(
×2×(![]() )
)
解得x=![]()
∴![]()
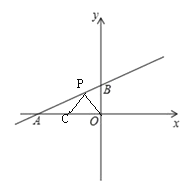
如图,当P点在直线AB上,当P在BA的延长线上,S△BOP>S△COP
故P在AB的延长线上,
设P(x,![]() )
)
∵![]() 和
和![]() 的面积相等
的面积相等
∴![]() BO×x=
BO×x= ![]() CO×(
CO×(![]() ),即
),即![]() ×2×x=
×2×x= ![]() ×2×(
×2×(![]() )
)
解得x=4
∴![]()
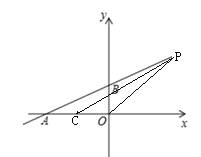
综上,![]() 或
或![]() ;
;
(3)∵过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,点
,点![]() 在直线
在直线![]() 上是
上是
∴设Q(-2,t),
∵A(-4,0),B(0,2)
∴AB2=20,AQ2=22+t2=4+t2,BQ2=22+(2-t)2=4+(2-t)2,
故当AB=BQ,即20=4+(2-t)2,
解得:t=-2或t=6
故Q![]()
故当AB=AQ,即20=4+t2,
解得:t=±4
故![]()
当AQ=BQ,即4+t2=4+(2-t)2,
解得:t=1
∵(-2,1)在直线y=![]() 上,故舍去
上,故舍去
∴Q点坐标为:![]()
![]() .
.


科目:初中数学 来源: 题型:
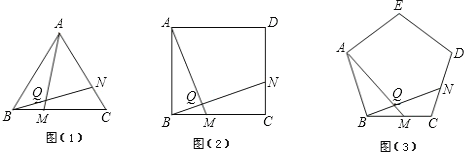
【题目】(1)如图(1),已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN.求出∠BQM的度数;
(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、…正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
正多边形 | 正方形 | 正五边形 | …… | 正n边形 |
∠BQM的度数 |
|
| …… |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上一点,
上一点,![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
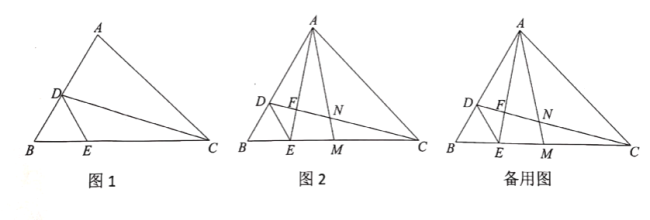
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,直接写出线段
,直接写出线段![]() ,
,![]() ,
,![]() 的等量关系.
的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.(1)甲蚂蚁选择“向左”爬行的概率为________;
(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),一架云梯AB斜靠在一竖直的墙上,云梯的顶端A距地面15米,梯子的长度比梯子底端B离墙的距离大5米.
(1)这个云梯的底端B离墙多远?
(2)如图(2),如果梯子的顶端下滑了8m(AC的长),那么梯子的底部在水平方向右滑动了多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网络约车公司近期推出了“520专享”服务计划,即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”,为进一步提升服务品质,公司监管部门决定了解“单次营运里程”的分布情况.老王收集了本公司的5 000个“单次营运里程”数据,这些里程数据均不超过25(公里),他从中随机抽取了200个数据作为一个样本,整理、统计结果如下表,并绘制了不完整的频数分布直方图.
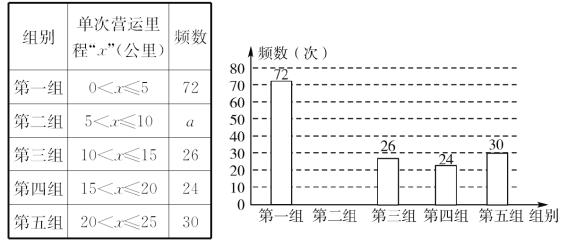
根据统计表、图提供的信息,解答下面的问题:
(1)表中a=________;样本中“单次营运里程”不超过15公里的频率为________;(2)请把频数分布直方图补充完整;
(3)请估计该公司这5 000个“单次营运里程”超过20公里的次数;
查看答案和解析>>
科目:初中数学 来源: 题型:
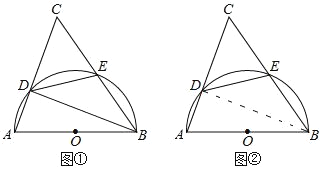
【题目】已知,△ABC中,∠A=68°,以AB为直径的⊙O与AC,BC的交点分别为D,E
(Ⅰ)如图①,求∠CED的大小;
(Ⅱ)如图②,当DE=BE时,求∠C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com