
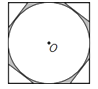
【题目】已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
A. 32![]() ﹣32﹣4πB.
﹣32﹣4πB. ![]() C. 1D. 16﹣4π
C. 1D. 16﹣4π
【答案】A
【解析】
连接OA、OB,作BI⊥OA于点I,作OM⊥AB于点M,求得△AOB的面积,则正八边形的面积即可求得,然后减去圆的面积即可求解.
解:连接OA、OB、JL、KM,作BI⊥OA于点I,作OM⊥AB于点M.
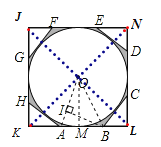
∵GF∥KN∥BC,AH∥JL∥DE,
∴△JGF, △KAH,CLB,END都是等腰直角三角形且全等,
∴∠HGF=∠GFE=∠FED=∠EDC=∠DCB=∠CBA=∠BAH=∠AHG=135°,
由切线长定理可知,GF=EF=DE=CD=BC=AB=AH=GH,
∴八边形ABCDEFGH是正八边形.
则∠AOB= ![]() =45°,
=45°,
∴△OBI是等腰直角三角形,
设AM=BM=x,则OA=OB=![]() ,OI=BI=
,OI=BI=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() (舍去),
(舍去),
∴AB=![]() ,
,
则S△AOB=![]() ABOM=
ABOM=![]() ×(
×(![]() )×2=4
)×2=4![]() -4,
-4,
则正八边形ABCDEFGH的面积是8(4![]() -4)=32
-4)=32![]() -32.
-32.
⊙O的面积是:4π,
则阴影部分的面积为:32![]() -32-4π.
-32-4π.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是⊙O的内接四边形,点F 是CD延长线上的一点,且AD平分∠BDF,AE⊥CD于点E.

⑴ 求证:AB=AC.
⑵ 若BD=11,DE=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①GH⊥BE;②△EHM∽△GHF;③![]() ﹣1;④
﹣1;④![]() =2﹣
=2﹣![]() ,其中正确的结论是( )
,其中正确的结论是( )
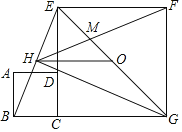
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某海域示意图,其中灯塔D的正东方向有一岛屿C.一艘快艇以每小时20nmile的速度向正东方向航行,到达A处时得灯塔D在东北方向上,继续航行0.3h,到达B处时测得灯塔D在北偏东30°方向上,同时测得岛屿C恰好在B处的东北方向上,此时快艇与岛屿C的距离是多少?(结果精确到1nmile.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
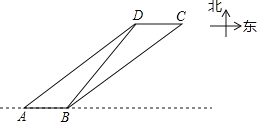
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.

(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
查看答案和解析>>
科目:初中数学 来源: 题型:
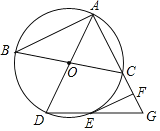
【题目】如图,△ABC内接于⊙O,AD与BC是⊙O的直径,延长线段AC至点G,使AG=AD,连接DG交⊙O于点E,EF∥AB交AG于点F.
(1)求证:EF与⊙O相切.
(2)若EF=2![]() ,AC=4,求扇形OAC的面积.
,AC=4,求扇形OAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,一次函数y=mx+n(m≠0)和二次函数y=ax2+bx+c(a≠0)的图象交于A(﹣3,0)和B两点,抛物线与x轴交于A、C两点,且C的横坐标在0到1之间(不含端点),下列结论正确的是( )
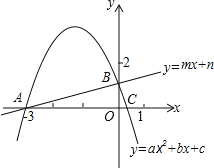
A. abc<0 B. 3a﹣b>0 C. 2a﹣b+m<0 D. a﹣b>2m﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
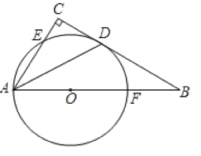
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E. F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com