
【题目】如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①GH⊥BE;②△EHM∽△GHF;③![]() ﹣1;④
﹣1;④![]() =2﹣
=2﹣![]() ,其中正确的结论是( )
,其中正确的结论是( )
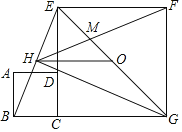
A. ①②③B. ①②④C. ①③④D. ②③④
【答案】A
【解析】
由四边形ABCD和四边形CGFE是正方形,得出△BCE≌△DCG,推出∠BEC+∠HDE=90°,从而得GH⊥BE;由GH是∠EGC的平分线,得出△BGH≌△EGH,再由O是EG的中点,利用中位线定理,得HO∥BG且HO=![]() BG;由△EHG是直角三角形,因为O为EG的中点,所以OH=OG=OE,得出点H在正方形CGFE的外接圆上,根据圆周角定理得出∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,从而证得△EHM∽△GHF;设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,由HO∥BG,得出△DHN∽△DGC,即可得出
BG;由△EHG是直角三角形,因为O为EG的中点,所以OH=OG=OE,得出点H在正方形CGFE的外接圆上,根据圆周角定理得出∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,从而证得△EHM∽△GHF;设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,由HO∥BG,得出△DHN∽△DGC,即可得出![]() ,得到
,得到![]() ,即a2+2ab-b2=0,从而求得
,即a2+2ab-b2=0,从而求得![]() ,设正方形ECGF的边长是2b,则EG=2
,设正方形ECGF的边长是2b,则EG=2![]() b,得到HO=
b,得到HO=![]() b,通过证得△MHO△MFE,得到
b,通过证得△MHO△MFE,得到![]() ,进而得到
,进而得到![]() ,进一步得到
,进一步得到![]() .
.
解:如图,
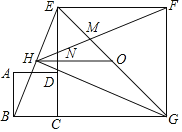
∵四边形ABCD和四边形CGFE是正方形,
∴BC=CD,CE=CG,∠BCE=∠DCG,
在△BCE和△DCG中,
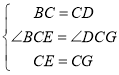
∴△BCE≌△DCG(SAS),
∴∠BEC=∠BGH,
∵∠BGH+∠CDG=90°,∠CDG=∠HDE,
∴∠BEC+∠HDE=90°,
∴GH⊥BE.
故①正确;
∵△EHG是直角三角形,O为EG的中点,
∴OH=OG=OE,
∴点H在正方形CGFE的外接圆上,
∵EF=FG,
∴∠FHG=∠EHF=∠EGF=45°,∠HEG=∠HFG,
∴△EHM∽△GHF,
故②正确;
∵△BGH≌△EGH,
∴BH=EH,
又∵O是EG的中点,
∴HO∥BG,
∴△DHN∽△DGC,
![]()
设EC和OH相交于点N.
设HN=a,则BC=2a,设正方形ECGF的边长是2b,则NC=b,CD=2a,
![]()
即a2+2ab﹣span>b2=0,
解得:a=b=(﹣1+![]() )b,或a=(﹣1﹣
)b,或a=(﹣1﹣![]() )b(舍去),
)b(舍去),
![]()
![]()
故③正确;
∵△BGH≌△EGH,
∴EG=BG,
∵HO是△EBG的中位线,
∴HO=![]() BG,
BG,
∴HO=![]() EG,
EG,
设正方形ECGF的边长是2b,
∴EG=2![]() b,
b,
∴HO=![]() b,
b,
∵OH∥BG,CG∥EF,
∴OH∥EF,
∴△MHO△MFE,
∴![]() ,
,
∴EM=![]() OM,
OM,
∴![]() ,
,
∴![]()
∵EO=GO,
∴S△HOE=S△HOG,
∴![]()
故④错误,
故选:A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,
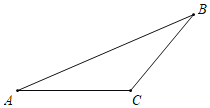
(1)按如下步骤尺规作图(保留作图痕迹):
①作AD平分∠BAC,交BC于D;
②作AD的垂直平分线MN分别交AB,AC于点E、F;
(2)连接DE、DF.若BD=12,AF=8,CD=6,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张矩形风景画,长为90cm,宽为60cm,现对该风景画进行装裱,得到一个新的矩形,要求其长、宽之比与原风景画的长、宽之比相同,且面积比原风景画的面积大44%.若装裱后的矩形的上、下边衬的宽都为acm,左、右边衬的宽都为bcm,那么ab=___cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是___;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B,…,按此规律,则矩形A4OC4B4的对称中心的坐标是___.
倍,得到矩形A2OC2B,…,按此规律,则矩形A4OC4B4的对称中心的坐标是___.
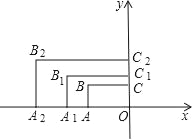
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】妈妈给小红和弟弟买了一本刘慈欣的小说《流浪地球》,姐弟俩都想先睹为快.是小红对弟弟说:我们利用下面中心涂黑的九宫格图案(如图所示)玩一个游戏,规则如下:我从第一行,你从第三行,同时各自任意选取一个方格,涂黑,如果得到的新图案是轴对称图形.我就先读,否则你先读.小红设计的游戏对弟弟是否公平?请用画树状图或列表的方法说明理由.(第一行的小方格从左至右分别用A,B,C表示,第三行的小方格从左至右分别用D,E,F表示)
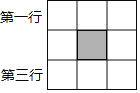
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
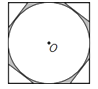
A. 32![]() ﹣32﹣4πB.
﹣32﹣4πB. ![]() C. 1D. 16﹣4π
C. 1D. 16﹣4π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y1=mx2-4mx+2n-1与平行于x轴的直线交于A、B两点,且A点坐标为(-1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,-1);③m>![]() ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是
;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是![]() ≤a<2;⑤不等式mx2-4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
≤a<2;⑤不等式mx2-4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
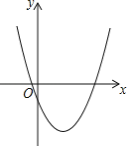
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com