
【题目】有一张矩形风景画,长为90cm,宽为60cm,现对该风景画进行装裱,得到一个新的矩形,要求其长、宽之比与原风景画的长、宽之比相同,且面积比原风景画的面积大44%.若装裱后的矩形的上、下边衬的宽都为acm,左、右边衬的宽都为bcm,那么ab=___cm2
科目:初中数学 来源: 题型:
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
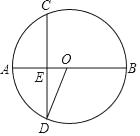
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接OD.
(1)过点C作射线CF交BA的延长线于点F,且使得∠ECF=∠AOD;(要求尺规作图,不写作法)
(2)求证:CF是⊙O的切线;
(3)若OE:AE=1:2,且AF=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的点A在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA=![]() ,则k的值为( )
,则k的值为( )

A. -3 B. -6 C. -4 D. -![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.
(1)甲组抽到A小区的概率是多少;
(2)请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
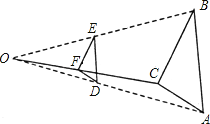
【题目】按如下方法,将△ABC的三边缩小的原来的![]() ,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
,如图,任取一点O,连AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法正确的个数是( )
①△ABC与△DEF是位似图形②△ABC与△DEF是相似图形
③△ABC与△DEF的周长比为1:2④△ABC与△DEF的面积比为4:1.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
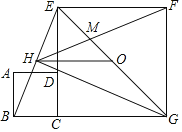
【题目】如图,正方形ABCD和正方形CGFE的顶点C,D,E在同一条直线上,顶点B,C,G在同一条直线上.O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接FH交EG于点M,连接OH.以下四个结论:①GH⊥BE;②△EHM∽△GHF;③![]() ﹣1;④
﹣1;④![]() =2﹣
=2﹣![]() ,其中正确的结论是( )
,其中正确的结论是( )
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.

(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑物,从10m高的窗口A,用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面![]() m,则水流落地点B离墙的距离OB是( )
m,则水流落地点B离墙的距离OB是( )
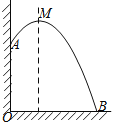
A.2mB.3mC.4mD.5m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com