
【题目】如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.

(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)连接OD,只需证明OD⊥DE.根据正方形的性质得到AE=AD,则∠ADE=45°.又∠ADO=45°则证明了结论;
(2)作OM⊥AB于M.根据平行线分线段成比例定理进行证明.
试题解析:证明:(1)连接OD.
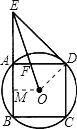
∵四边形ABCD为正方形,AE=AB.
∴AE=AB=AD,∠EAD=∠DAB=90°,
∴∠EDA=45°,∠ODA=45°,
∴∠ODE=∠ADE+∠ODA=90°,
∴直线ED是⊙O的切线.
(2)作OM⊥AB于M,
∵O为正方形的中心,
∴M为AB中点,
∴AE=AB=2AM,AF∥OM,
∴![]()
∴EF=2FO.
(2)作OM⊥AB于M.根据平行线分线段成比例定理进行证明.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为( )
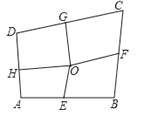
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为________;
(2)该同学从5个项目中任选两个,利用树状图或列表列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
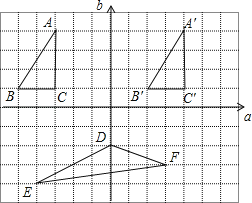
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点△A′B′C′是由格点△ABC通过怎样的变换得到的?
(2)如果以直线a、b为坐标轴建立平面直角坐标系后,点A的坐标为(﹣3,4),请写出格点△DEF各顶点的坐标,并求出△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉兴市2010~2014年社会消费品零售总额及增速统计图如下:
请根据图中信息,解答下列问题:
(1)求嘉兴市2010~2014年社会消费品零售总额增速这组数据的中位数.
(2)求嘉兴市近三年(2012~2014年)的社会消费品零售总额这组数据的平均数.
(3)用适当的方法预测嘉兴市2015年社会消费品零售总额(只要求列出算式,不必计算出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过P(-2·3).
(1)求此反比例函数的解析式;
(2)点A(2.-3)、B(3,2)是否在这个函数的图象上?
(3)这个函数的图象位于哪些象限?函数值y随自变量x的减小如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题:
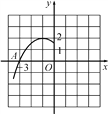
(1)抛物线与x轴的一个交点A的坐标是 ,则抛物线与x轴的另一个交点B的坐标是 ;
(2)确定a的值;
(3)设抛物线的顶点是P,试求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解决问题:
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
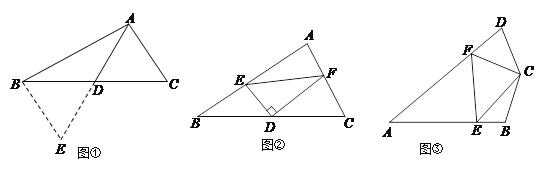
(1)如图①,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com