
【题目】如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题:
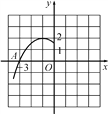
(1)抛物线与x轴的一个交点A的坐标是 ,则抛物线与x轴的另一个交点B的坐标是 ;
(2)确定a的值;
(3)设抛物线的顶点是P,试求△PAB的面积.
【答案】(1)(-3,0),(1,0) ;(2) a=-![]() ;(3)4.
;(3)4.
【解析】试题分析:(1)由图象可求得A点的坐标,由解析式可求得抛物线的对称轴方程,利用图象的对称性可求得B点坐标;
(2)把B点坐标代入抛物线解析式可求得a的值;
(3)由抛物线解析式可求得P点坐标,再结合A、B坐标可求得AB的值,则可求得△PAB的面积.
试题解析:(1)由图象可知A点坐标为(3,0),
∵y=a(x+1)2+2,
∴抛物线对称轴方程为x=1,
∵A、B两点关于对称轴对称,
∴B的坐标为(1,0),
故答案为:(3,0);(1,0);
(2)将(1,0)代入y=a(x+1)2+2,
可得0=4a+2,解得a=-![]() ;
;
(3)∵y=a(x+1)2+2,
∴抛物线的顶点坐标是(-1,2),
∵A(-3,0),B(1,0),
∴AB=1-(-3)=4,
∴S△PAB=![]() ×4×2=4.
×4×2=4.


科目:初中数学 来源: 题型:
【题目】不解方程,求下列各方程的两根之和与两根之积:
(1)x2+2x+1=0; (2)3x2-2x-1=0; (3)2x2+3=7x2+x; (4)5x-5=6x2-4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是⊙O的内接正方形,延长BA到E,使AE=AB,连接ED.

(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于点F,求证:EF=2FO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A. ![]() B. 3 C. 1 D.
B. 3 C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
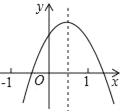
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0;⑤4ac﹣b2<0,正确的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com