
【题目】(1)已知a+b=7,ab=10,求a2+b2,(a-b)2的值;
(2)先化简(![]() -
-![]() )÷
)÷![]() ,并回答:原代数式的值可以等于-1吗?为什么?
,并回答:原代数式的值可以等于-1吗?为什么?
【答案】(1)a2+b2=29, (a-b)2=9;(2)原代数式的值不能等于-1,理由见解析.
【解析】试题分析:(1)根据完全平方公式,即可解答;
(2)原式括号中两项约分后,利用乘法分配律化简,约分后利用同分母分式的减法法则计算得到最简结果,令原式的值为-1,求出x的值,代入原式检验即可得到结果.
试题解析:(1)a2+b2=(a+b)2-2ab=72-2×10=49-20=29, (a-b)2=(a+b)2-4ab=72-4×10=49-40=9.
(2) 原式=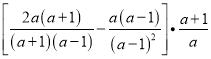
=![]()
=![]() ,
,
原式的值为-1,即![]() =-1,
=-1,
去分母得:a+1=-a+1,
解得:a=0,
代入原式检验,分母为0,不合题意,
则原式的值不可能为-1.


科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:
径赛项目:100m,200m,400m(分别用A1、A2、A3表示);
田赛项目:跳远,跳高(分别用B1、B2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率为________;
(2)该同学从5个项目中任选两个,利用树状图或列表列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过P(-2·3).
(1)求此反比例函数的解析式;
(2)点A(2.-3)、B(3,2)是否在这个函数的图象上?
(3)这个函数的图象位于哪些象限?函数值y随自变量x的减小如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题:
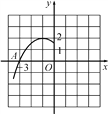
(1)抛物线与x轴的一个交点A的坐标是 ,则抛物线与x轴的另一个交点B的坐标是 ;
(2)确定a的值;
(3)设抛物线的顶点是P,试求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
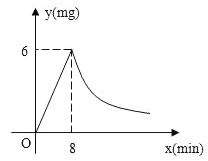
【题目】为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( ).

A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(![]() )求抛物线的解析式.
)求抛物线的解析式.
(![]() )设抛物线的顶点为
)设抛物线的顶点为![]() ,点
,点![]() 在抛物线的对称轴上,且
在抛物线的对称轴上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(![]() )点
)点![]() 在直线
在直线![]() 上方的抛物线上,是否存在点
上方的抛物线上,是否存在点![]() 使
使![]() 的面积最大,若存在,请求出点
的面积最大,若存在,请求出点![]() 坐标.
坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解决问题:
截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
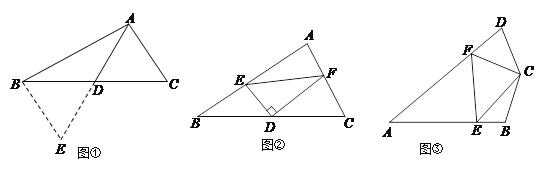
(1)如图①,在△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com