
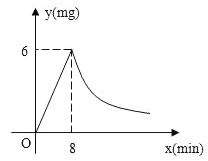
【题目】为了预防“甲型H1N1”,某学校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
【答案】(1)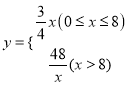 ;(2)30;(3)这次消毒是有效的.
;(2)30;(3)这次消毒是有效的.
【解析】试题分析: (1)药物燃烧时,设出y与x之间的解析式y=k1x,把点(8,6)代入即可,从图上读出x的取值范围;药物燃烧后,设出y与x之间的解析式y=![]() ,把点(8,6)代入即可;
,把点(8,6)代入即可;
(2)把y=1.6代入反比例函数解析式,求出相应的x;
(3)把y=3代入正比例函数解析式和反比例函数解析式,求出相应的x,两数之差与10进行比较,>等于10就有效.
试题解析:
解:(1)设药物燃烧时y关于x的函数关系式为y=k1x(k1>0)代入(8,6)为6=8k1
∴k1=![]()
设药物燃烧后y关于x的函数关系式为y=![]() (k2>0)代入(8,6)为6=
(k2>0)代入(8,6)为6=![]() ,
,
∴k2=48
∴药物燃烧时y关于x的函数关系式为![]() (0≤x≤8)药物燃烧后y关于x的函数关系式为
(0≤x≤8)药物燃烧后y关于x的函数关系式为![]() (x>8)
(x>8)
∴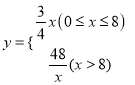
(2)结合实际,令![]() 中y≤1.6得x≥30
中y≤1.6得x≥30
即从消毒开始,至少需要30分钟后学生才能进入教室.
(3)把y=3代入![]() ,得:x=4
,得:x=4
把y=3代入![]() ,得:x=16
,得:x=16
∵16﹣4=12
所以这次消毒是有效的.
点睛: 现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.


科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.

(1)根据上表数据估计从袋中摸出一个球是黑球的概率是________;
(2)估算袋中白球的个数;
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )
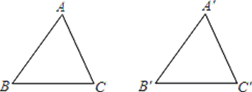
A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为( )

A. ![]() B. 3 C. 1 D.
B. 3 C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金瑞公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.
(1)求金瑞公司至少购进甲型显示器多少台?
(2)若甲型显示器的台数不超过乙型显示器的台数,则有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆![]() 与地面仍保持垂直的关系,而折断部分
与地面仍保持垂直的关系,而折断部分![]() 与未折断树杆
与未折断树杆![]() 形成
形成![]() 的夹角.树杆
的夹角.树杆![]() 旁有一座与地面垂直的铁塔
旁有一座与地面垂直的铁塔![]() ,测得
,测得![]() 米,塔高
米,塔高![]() 米.在某一时刻的太阳照射下,未折断树杆
米.在某一时刻的太阳照射下,未折断树杆![]() 落在地面的影子
落在地面的影子![]() 长为
长为![]() 米,且点
米,且点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,点
在同一条直线上,点![]() 、
、![]() 、
、![]() 也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到
也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到![]() ,参考数据:
,参考数据: ![]() ,
, ![]() ,
, ![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
“![]() ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如: ![]() ,
,
∵![]() ≥0,
≥0,
∴![]() ≥1,
≥1,
∴![]() ≥1.
≥1.
试利用“配方法”解决下列问题:
(1)填空: ![]() (x )2+ ;
(x )2+ ;
(2) 已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
(3)比较代数式![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com