
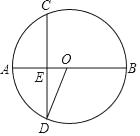
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接OD.
(1)过点C作射线CF交BA的延长线于点F,且使得∠ECF=∠AOD;(要求尺规作图,不写作法)
(2)求证:CF是⊙O的切线;
(3)若OE:AE=1:2,且AF=6,求⊙O的半径.
【答案】(1)见解析(2)证明见解析(3)3
【解析】
(1)连接OC,根据尺规作图方法,作∠ECF=∠AOD,交BA的延长线于点F即可.
(2)通过证明∠OCF=90°即可.
(3),由OE:AE=1:2可知OA=3AE,由△OCE∽△OFC可知OF=3OC,可求出OE的长度进而求出OA即可.
(1)解:如图直线CF即为所求;
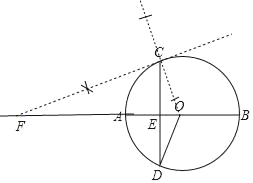
(2)∵OC=OD
∴∠OCE=∠ODE
∵CD⊥AB
∴∠DOE+∠ODE=90°
∵∠ECF=∠AOD,∠OCE=∠ODE
∴∠OCE+∠ECF=90°,即∠OCF=90°,
∴直线CF是⊙O的切线.
(3)解:设OE=a,则AE=2a,OC=OA=3a.
∵△OCE∽△OFC,
∴![]()
∴OF=3OC,
∴6+3a=9a,
∴a=1,
∴OC=3.


科目:初中数学 来源: 题型:
【题目】![]() 和△A′B′C′在平面直角坐标系中的位置分别如图所示.
和△A′B′C′在平面直角坐标系中的位置分别如图所示.
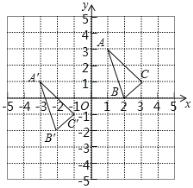
(1)分别写出下列各点的坐标:A ;B ;C ;
(2)△A′B′C′由 ![]() 经过怎样的平移得到?并写出点A′,B′,C′的坐标.
经过怎样的平移得到?并写出点A′,B′,C′的坐标.
(3)求![]() 面积.
面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.
下列四种说法:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.
其中,正确的有( ) 个.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角![]() 中,
中,![]() ,若想找一点P,使得
,若想找一点P,使得![]() 与
与![]() 互补,甲、乙、丙三人作法分别如下:
互补,甲、乙、丙三人作法分别如下:
甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求;
乙:分别以B,C为圆心,AB,AC长为半径画弧交于P点,则P即为所求;
丙:作BC的垂直平分线和![]() 的平分线,两线交于P点,则P即为所求.
的平分线,两线交于P点,则P即为所求.
对于甲、乙、丙三人的作法,下列叙述正确的是![]()
![]()

A. 三人皆正确B. 甲、丙正确,乙错误
C. 甲正确,乙、丙错误D. 甲错误,乙、丙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于![]() 的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为( )
的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为( )

A.100°B.110°C.120°D.130°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条抛物线的开口大小与方向、对称轴均与抛物线y=![]() x2相同,并且抛物线经过点(1,1).
x2相同,并且抛物线经过点(1,1).
(1)求抛物线的解析式,并指明其顶点;
(2)所求抛物线如何由抛物线y=![]() x2平移得到?
x2平移得到?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com