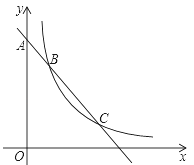
【题目】如图，一次函数y=k1x+b的图象过点A（0，3），且与反比例函数y=
的图象相交于B、C两点．若AB=BC，则k1k2的值为_____．
【答案】﹣2．
【解析】
设一次函数的解析式为y=k1x+3，反比例函数解析式y=
，都经过B点，得等式k1x+3﹣=0，再由AB=BC，得到点C的横坐标是点B横坐标的2倍，不防设x2=2x1，列出x1，x2关系等式，据此可以求出k1·k2的值．
k1k2=﹣2，是定值．理由如下：
∵一次函数y=k1x+b的图象过点A（0，3），
∴设一次函数的解析式为y=k1x+3，反比例函数解析式y=，
∴k1x+3=，
整理得k1x2+3x﹣k2=0，
∴x1+x2=﹣
，x1x2=﹣，
∵AB=BC，
∴点C的横坐标是点B横坐标的2倍，不防设x2=2x1，
∴x1+x2=3x1=﹣，x1x2=2x12=﹣
，
∴﹣
，
整理得，k1k2=﹣2，是定值．
故答案为﹣2．
轻松课堂单元期中期末专题冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】如图，已知△ABC与△CDE都是等边三角形，AD与BE相交于点G，BE与AC相交于点F，AD与CE相交于点H，则下列结论：①△ACD≌△BCE；②∠AFB=60°；③BF=AH；④△ECF≌△DCG；⑤连CG，则∠BGC=∠DGC.其中正确的个数是（）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小明家窗外有一堵围墙AB，由于围墙的遮挡，清晨太阳光恰好从窗户的最高点C射进房间的地板F处，中午太阳光恰好能从窗户的最低点D射进房间的地板E处，小明测得窗子距地面的高度OD＝0.8 m，窗高CD＝1.2 m，并测得OE＝0.8 m，OF＝3 m，求围墙AB的高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，则符合这一结果的实验最有可能的是（ ）
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0．365 | 0．328 | 0．330 | 0．334 | 0．336 | 0．332 | 0．333 |
A．一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃
B．在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀”
C．抛一个质地均匀的正六面体骰子，向上的面点数是5
D．抛一枚硬币，出现反面的概率
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有五张正面分别写有数字﹣3，﹣2，1， 2，3的卡片，它们的背面完全相同，现将这五张卡片背面朝上洗匀后随机抽取一张，以其正面的数字作为a的值，然后再从剩余的四张卡片中随机抽取一张，以其正面的数字作为b的值，用列表法或树状图法求点（a，b）在反比例函数y=
图象上的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了方便孩子入学，小王家购买了一套学区房，交首付款15万元，剩余部分向银行贷款，贷款及贷款利息按月分期还款，每月还款数相同．计划每月还款y万元，x个月还清贷款，若y是x的反比例函数，其图象如图所示：
（1）求y与x的函数解析式；
（2）若小王家计划180个月（15年）还清贷款，则每月应还款多少万元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，点A和点B分别在y轴正半轴和x轴负半轴上，且OA=OB，点C和点D分别在第四象限和第一象限，且OC⊥OD，OC=OD，点D的坐标为（m，n），且满足
+|n﹣2|=0．
（1）求点D的坐标；（2）求∠AKO的度数；（3）如图2，点P，Q分别在y轴正半轴和x轴负半轴上，且OP=OQ，直线ON⊥BP交AB于点N，MN⊥AQ交BP的延长线于点M，判断ON，MN，BM的数量关系并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
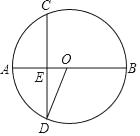
【题目】如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接OD．
（1）过点C作射线CF交BA的延长线于点F，且使得∠ECF=∠AOD；（要求尺规作图，不写作法）
（2）求证：CF是⊙O的切线；
（3）若OE：AE=1：2，且AF=6，求⊙O的半径．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
