
【题目】如图1,点A和点B分别在y轴正半轴和x轴负半轴上,且OA=OB,点C和点D分别在第四象限和第一象限,且OC⊥OD,OC=OD,点D的坐标为(m,n),且满足![]() +|n﹣2|=0.
+|n﹣2|=0.
(1)求点D的坐标;(2)求∠AKO的度数;(3)如图2,点P,Q分别在y轴正半轴和x轴负半轴上,且OP=OQ,直线ON⊥BP交AB于点N,MN⊥AQ交BP的延长线于点M,判断ON,MN,BM的数量关系并证明.

【答案】(1)(4,2);(2)135°;(3)见解析.
【解析】
(1)利用非负数的性质即可解决问题;(2)如图1中,作OE⊥BD于E,OF⊥AC于F.只要证明△BOD≌△AOC,推出EO=OF(全等三角形对应边上的高相等),推出OK平分∠BKC,再证明∠AKB=∠BOA=90°,即可解决问题;(3)结论:BM=MN+ON;只要证明△BNH≌△BNO,以及MH=MB即可解决问题;
解:(1)∵![]() =0,
=0,
又∵![]() ≥0,|n﹣2|≥0,
≥0,|n﹣2|≥0,
∴n=2,m=4,
∴点D坐标为(4,2).
(2)如图1中,作OE⊥BD于E,OF⊥AC于F.
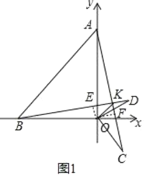
∵OA=OB,OD=OC,∠AOB=∠COD=90°,
∴∠BOD=∠AOC,
∴△BOD≌△AOC,
∴EO=OF(全等三角形对应边上的高相等),
∴OK平分∠BKC,
∴∠OBD=∠OAC,易证∠AKB=∠BOA=90°,
∴∠OKE=45°,
∴∠AKO=135°.
(3)结论:BM=MN+ON.
理由:如图2中,过点B作BH∥y轴交MN的延长线于H.
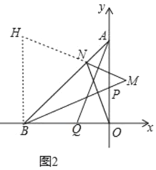
∵OQ=OP,OA=OB,∠AOQ=∠BOP=90°,
∴△AOQ≌△BOP,
∴∠OBP=∠OAQ,
∵∠OBA=∠OAB=45°,
∴∠ABP=∠BAQ,
∵NM⊥AQ,BM⊥ON,
∴∠ANM+∠BAQ=90°,∠BNO+∠ABP=90°,
∴∠ANM=∠BNO=∠HNB,
∵∠HBN=∠OBN=45°,BN=BN,
∴△BNH≌△BNO,
∴HN=NO,∠H=∠BON,
∵∠HBM+∠MBO=90°,∠BON+∠MBO=90°,
∴∠HBM=∠BON=∠H,
∴MH=MB,
∴BM=MN+NH=MN+ON.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再完成练习

一般地,数轴上表示数x的点与原点的距离,叫做数x的绝对值,记作|x|.
|x|<3
x表示到原点距离小于3的数,从如图1所示的数轴上看:大于﹣3而小于3的数,它们到原点距离小于3,所以|x|<3的解集是﹣3<x<3;
|x|>3
x表示到原点距离大于3的数,从如图2所示的数轴上看:小于﹣3的数或大于3的数,它们到原点距离大于3,所以x>3的解集是x<﹣3或x>3
解答下面的问题:
(1)不等式|x|<5的解集为 ,不等式|x|>5的解集为 .
(2)不等式|x|<m(m>0)的解集为 .不等式|x|>m(m>0)的解集为 .
(3)解不等式|x﹣3|<5.
(4)解不等式|x﹣5|>3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )

A. β﹣α=60° B. β+α=210° C. β﹣2α=30° D. β+2α=240°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,∠A=30°,点P从点A出发以2m/s的速度沿折线A→C→B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1,C2两段组成,如图2所示,下列结论中,错误的是( )

A. α=1
B. sinB=![]()
C. △APQ面积的最大值为2
D. 图2中图象C2段的函数表达式为y=﹣![]() x2+
x2+![]() x
x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 和△A′B′C′在平面直角坐标系中的位置分别如图所示.
和△A′B′C′在平面直角坐标系中的位置分别如图所示.
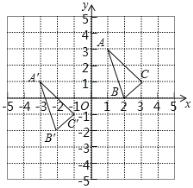
(1)分别写出下列各点的坐标:A ;B ;C ;
(2)△A′B′C′由 ![]() 经过怎样的平移得到?并写出点A′,B′,C′的坐标.
经过怎样的平移得到?并写出点A′,B′,C′的坐标.
(3)求![]() 面积.
面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于E、F两点;再分别以E、F为圆心,大于![]() 的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为( )
的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠CMA=25°,则∠C的度数为( )

A.100°B.110°C.120°D.130°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com