
【题目】![]() 和△A′B′C′在平面直角坐标系中的位置分别如图所示.
和△A′B′C′在平面直角坐标系中的位置分别如图所示.
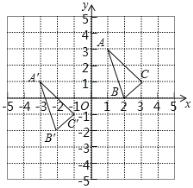
(1)分别写出下列各点的坐标:A ;B ;C ;
(2)△A′B′C′由 ![]() 经过怎样的平移得到?并写出点A′,B′,C′的坐标.
经过怎样的平移得到?并写出点A′,B′,C′的坐标.
(3)求![]() 面积.
面积.
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A和点B分别在y轴正半轴和x轴负半轴上,且OA=OB,点C和点D分别在第四象限和第一象限,且OC⊥OD,OC=OD,点D的坐标为(m,n),且满足![]() +|n﹣2|=0.
+|n﹣2|=0.
(1)求点D的坐标;(2)求∠AKO的度数;(3)如图2,点P,Q分别在y轴正半轴和x轴负半轴上,且OP=OQ,直线ON⊥BP交AB于点N,MN⊥AQ交BP的延长线于点M,判断ON,MN,BM的数量关系并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
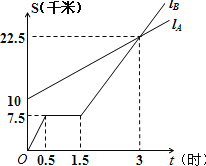
(1)B出发时与A相距 千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备销售甲、乙两种商品共 80 件,已知 2 件甲种商品 与 3 件乙种商品的销售利润相同,3 件甲种商品比 2 件乙商品的销售利润多 150 元。
(1)每件甲种商品与每件乙种商品的销售利润各多少元?
(2)若甲、乙两种商品的销售总利润不低于 6600 元,则至少销售甲种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
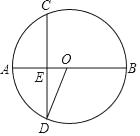
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接OD.
(1)过点C作射线CF交BA的延长线于点F,且使得∠ECF=∠AOD;(要求尺规作图,不写作法)
(2)求证:CF是⊙O的切线;
(3)若OE:AE=1:2,且AF=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(图1,图2),四边形ABCD是边长为4的正方形,点E在线段BC上,∠AEF=90°,且EF交正方形外角平分线CP于点F,交BC的延长线于点N, FN⊥BC.
(1)若点E是BC的中点(如图1),AE与EF相等吗?
(2)点E在BC间运动时(如图2),设BE=x,△ECF的面积为y。
①求y与x的函数关系式;
②当x取何值时,y有最大值,并求出这个最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com