
【题目】如图,在△ABC中,点D、E、F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.
下列四种说法:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.
其中,正确的有( ) 个.

A.1 B.2 C.3 D.4
【答案】D
【解析】
试题分析:先由两组对边分别平行的四边形为平行四边形,根据DE∥CA,DF∥BA,得出AEDF为平行四边形,得出①正确;当∠BAC=90°,根据推出的平行四边形AEDF,利用有一个角为直角的平行四边形为矩形可得出②正确;若AD平分∠BAC,得到一对角相等,再根据两直线平行内错角相等又得到一对角相等,等量代换可得∠EAD=∠EDA,利用等角对等边可得一组邻边相等,根据邻边相等的平行四边形为菱形可得出③正确;由AB=AC,AD⊥BC,根据等腰三角形的三线合一可得AD平分∠BAC,同理可得四边形AEDF是菱形,④正确,进而得到正确说法的个数.
解:∵DE∥CA,DF∥BA,
∴四边形AEDF是平行四边形,选项①正确;
若∠BAC=90°,
∴平行四边形AEDF为矩形,选项②正确;
若AD平分∠BAC,
∴∠EAD=∠FAD,
又DE∥CA,∴∠EDA=∠FAD,
∴∠EAD=∠EDA,
∴AE=DE,
∴平行四边形AEDF为菱形,选项③正确;
若AB=AC,AD⊥BC,
∴AD平分∠BAC,
同理可得平行四边形AEDF为菱形,选项④正确,
则其中正确的个数有4个.
故选D.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
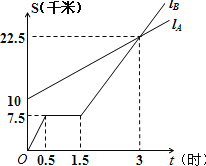
(1)B出发时与A相距 千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是 小时.
(3)B出发后 小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备销售甲、乙两种商品共 80 件,已知 2 件甲种商品 与 3 件乙种商品的销售利润相同,3 件甲种商品比 2 件乙商品的销售利润多 150 元。
(1)每件甲种商品与每件乙种商品的销售利润各多少元?
(2)若甲、乙两种商品的销售总利润不低于 6600 元,则至少销售甲种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某健身房的普通卡票价为20元/张,为了促销,新推出两种优惠卡仅限11月12月使用;①金卡售价为600元/张,每次凭卡不再收费;②银卡售价为150元/张,每次凭卡另收10元;设顾客去健身房的次数为x次,用普通票消费是y1元,用金卡消费是y2元,用银卡消费是y3元;

(1) 分别写出y1、y2、y3与x的关系式;(不写x的取值范围)
(2)根据所给图形,分别说出当x为多少次时,普通票更优惠?多少次时,银卡更优惠?多少次时,金卡更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
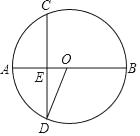
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接OD.
(1)过点C作射线CF交BA的延长线于点F,且使得∠ECF=∠AOD;(要求尺规作图,不写作法)
(2)求证:CF是⊙O的切线;
(3)若OE:AE=1:2,且AF=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM,下列结论:①AE=AF;②DF=DN;③AE=CN;④△AMD和△DMN的面积相等,其中错误的结论个数是( )

A.3个B.2个C.1个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(2)班课题研究小组对本校初三段全体同学的体育达标(体育成绩60分以上,含60分)情况进行调查,他们对本班50名同学的体育达标情况和其余班级同学的体育达标情况分别进行调查,数据统计如下:
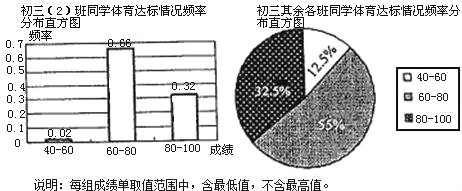
根据以上统计图,请解答下面问题:
(1)初三(2)班同学体育达标率和初三段其余班级同学达标率各是多少?
(2)如果全段同学的体育达标率不低于90%,则全段同学人数不超过多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com