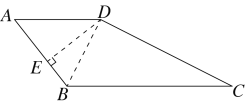
[题目]如图.四边形ABCD中.AB=AD=2.∠A=60°.BC=.CD=3．(1)求∠ADC的度数,(2)求四边形ABCD的面积．题目和参考答案 ——青夏教育精英家教网—

【题目】如图，四边形ABCD中，AB=AD=2，∠A=60°，BC=，CD=3．

（1）求∠ADC的度数；

（2）求四边形ABCD的面积．

参考答案：

【答案】（1）150°；（2）

【解析】

（1）连接BD，由一个角是60°的等腰三角形是等边三角形可判定△ABD为等边三角形，然后由勾股定理逆定理判定△BCD为直角三角形，即可求出∠ADC；

（2）分别计算等边三角形面积和直角三角形面积求和即可.

解：(1) 连接BD

∵∠A=60°，AB=AD，∴△ABD为等边三角形

∴BD=AB=2，

∴BD2+CD2=4+9=13，BC2=13, ∴BD2+CD2=13=BC2，

∴∠BDC=90°，∴∠ADC=90° + 60°=150°

(2)作DE⊥AB于E,则∠DEB=90°，∴BE=1, ，

∴S四边形ABCD= S△DBC + S△ABD =×2×3+×2×=

相关试题

科目： 来源： 题型：

【题目】已知，抛物线与x轴正半轴交于A、B两点（A点在B点左边），且AB=4．
（1）求k值；
（2）该抛物线与直线交于C、D两点，求S△ACD；
（3）该抛物线上是否存在不同于A点的点P，使S△PCD=S△ACD？若存在，求出P点坐标．
（4）若该抛物线上有点P，使S△PCD=tS△ACD，抛物线上满足条件的P点有2个，3个，4个时，分别直接写出t的取值范围．
查看答案和解析>>
科目： 来源： 题型：

【题目】作图题：
如图，在10×10的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）．
（1）在图中画出△ABC关于直线l对称的△A1B1C1；
（要求：A与A1，B与B1，C与C1相对应）
（2）求出△A1B1C1面积．
（3）在直线l上找一点P，使得PA+PB的值最小.
查看答案和解析>>
科目： 来源： 题型：

【题目】已知a≠0，在同一直角坐标系中，函数y=ax与y=ax2的图象有可能是（　　）
A. B. C. D.
查看答案和解析>>
科目： 来源： 题型：

【题目】（1）如图（1），已知△ABC,以AB、AC为边向△ABC外作等边三角形ABD和等边三角形ACE，连接BE、CD.请你完成图形，并证明：BE=CD;
（2）如图（2），已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,BE和CD有什么数量关系？说明理由；
（3）运用(1)(2)解答中所积累的经验和知识，完成下题：如图（3），要测量河两岸相对的两点B、E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC=1千米，AC=AE.求BE的长.
查看答案和解析>>
科目： 来源： 题型：

【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28 m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=x m．若在P处有一棵树与墙CD，AD的距离分别是15 m和6 m，要将这棵树围在花园内（含边界，不考虑树的粗细），则花园面积S的最大值为（）
A. 196 B. 195 C. 132 D. 14
查看答案和解析>>
科目： 来源： 题型：

【题目】如图1，在长方形中，，有一只蚂蚁在点处开始以每秒1个单位的速度沿边向点爬行，另一只蚂蚁从点以每秒2个单位的速度沿边向点爬行，蚂蚁的大小忽略不计，如果、同时出发，设运动时间为s.
(1)当时，求的面积;
(2)当时，试说明是直角二角形;
(3)当运动3s时，点停止运动，点以原速立即向点返回，在返回的过程中，是否存在点，使得平分?若存在，求出点运动的时间，若不存在请说明理由.
查看答案和解析>>