Question

【题目】如图，抛物线y=ax2+bx+与直线AB交于点A（﹣1，0），B（4，），点D是抛物线A、B两点间部分上的一个动点（不与点A、B重合），直线CD与y轴平行，交直线AB于点C，连接AD，BD．

（1）求抛物线的表达式；

（2）设点D的横坐标为m，△ADB的面积为S，求S关于m的函数关系式，并求出当S取最大值时的点C的坐标．

Answer 1

【答案】（1）y=﹣x2+2x+(2) C（ ， ）

【解析】分析: （1）将点A、B的坐标代入抛物线的解析式，求得a、b的值，从而得到抛物线的解析式；

（2）设直线AB为：y=kx+b．将A、B的坐标代入可得到k，b的方程组，从而可求得k，b于是得到直线AB的解析式，记CD与x轴的交点坐标为E．过点B作BF⊥DC，垂足为F．设D（m，﹣m2+2m+）则C（m，m+），依据三角形的面积公式可得到S与m的函数关系式，接下来由抛物线的对称轴方程，可求得m的值，于是可得到点C的坐标．

详解:

（1）∵由题意得,解得：，

∴y=﹣x2+2x+．

（2）设直线AB为：y=kx+b．则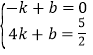，解得

直线AB的解析式为y=+．

如图所示：记CD与x轴的交点坐标为E．过点B作BF⊥DC，垂足为F．

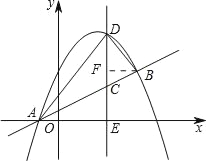
设D（m，﹣m2+2m+）则C（m，m+）．

∵CD=（﹣m2+2m+）﹣（m+）=m2+m+2，

∴S=AEDC+CDBF=CD（AE+BF）=DC=m2+m+5．

∴S=m2+m+5．

∵﹣＜0，

∴当m=时，S有最大值．

∴当m=时，m+=×+=．

∴点C（，）．

点睛: 本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求一次函数、二次函数的解析式、三角形的面积公式、二次函数的性质，用含m的式子表示出CD的长，从而得到S与m的关系式是解题的关键．