
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНx2ЃЋmxЃЋnОЙ§ЕуA(3ЃЌ0)ЁЂ
B(0ЃЌЃ3)ЃЌЕуPЪЧжБЯпABЩЯЕФЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпНЛХзЮяЯпгкЕуMЃЌЩшЕуPЕФКс
зјБъЮЊtЃЎ
(1)ЗжБ№ЧѓГіжБЯпABКЭетЬѕХзЮяЯпЕФНтЮіЪНЃЎ
(2)ШєЕуPдкЕкЫФЯѓЯоЃЌСЌНгAMЁЂBMЃЌЕБЯпЖЮPMзюГЄЪБЃЌЧѓЁїABMЕФУцЛ§ЃЎ
(3)ЪЧЗёДцдкетбљЕФЕуPЃЌЪЙЕУвдЕуPЁЂMЁЂBЁЂOЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуPЕФКсзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПНтЃК(1)АбAЃЈ3ЃЌ0ЃЉBЃЈ0ЃЌ-3ЃЉДњШы![]() ЃЌЕУ
ЃЌЕУ
![]() НтЕУ
НтЕУ![]()
ЫљвдХзЮяЯпЕФНтЮіЪНЪЧ![]() .
.
ЩшжБЯпABЕФНтЮіЪНЪЧ![]() ,АбAЃЈ3ЃЌ0ЃЉBЃЈ0ЃЌ
,АбAЃЈ3ЃЌ0ЃЉBЃЈ0ЃЌ![]() ЃЉДњШы
ЃЉДњШы![]() ,ЕУ
,ЕУ
![]() НтЕУ
НтЕУ![]()
ЫљвджБЯпABЕФНтЮіЪНЪЧ![]() .
.
(2)ЩшЕуPЕФзјБъЪЧЃЈ![]() ЃЉ,дђMЃЈ
ЃЉ,дђMЃЈ![]() ,
,![]() ЃЉ,вђЮЊ
ЃЉ,вђЮЊ![]() дкЕкЫФЯѓЯоЃЌЫљвдPM=
дкЕкЫФЯѓЯоЃЌЫљвдPM=![]() ЃЌЕБPMзюГЄЪБ
ЃЌЕБPMзюГЄЪБ![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]()
![]() =
=![]() =
=![]() .
.
ЃЈ3ЃЉШєДцдкЃЌдђПЩФмЪЧЃК
ЂйPдкЕкЫФЯѓЯоЃКЦНааЫФБпаЮOBMP ,PM=OB=3ЃЌ PMзюГЄЪБ![]() ЃЌЫљвдВЛПЩФм.
ЃЌЫљвдВЛПЩФм.
ЂкPдкЕквЛЯѓЯоЦНааЫФБпаЮOBPMЃК PM=OB=3ЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉЃЌЫљвдPЕуЕФКсзјБъЪЧ
ЃЈЩсШЅЃЉЃЌЫљвдPЕуЕФКсзјБъЪЧ![]() .
.
ЂлPдкЕкШ§ЯѓЯоЦНааЫФБпаЮOBPMЃКPM=OB=3ЃЌ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ЫљвдPЕуЕФКсзјБъЪЧ![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁПТд



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
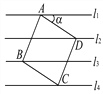
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЁЮl3ЁЮl4ЃЌЯрСкСНЬѕЦНаажБЯпМфЕФОрРыЖМЪЧ1.ШчЙће§ЗНаЮABCDЕФЫФИіЖЅЕуЗжБ№дкЫФЬѕжБЯпЩЯЃЌФЧУДsinІСЃНЃпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЫФБпаЮABCDжаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌACгыBDНЛгкЕуFЃЎ
ЃЌACгыBDНЛгкЕуFЃЎ

(1) ШчЭМ1ЃЌЧѓжЄЃКХаЖЯ![]() ЕФаЮзДВЂжЄУїФуЕФНсТл
ЕФаЮзДВЂжЄУїФуЕФНсТл
(2) ШчЭМ2ЃЌШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌВТЯыЃК
ЃЌВТЯыЃК![]() КЭ
КЭ![]() ЕФЪ§СПЙиЯЕВЂжЄУї
ЕФЪ§СПЙиЯЕВЂжЄУї
(3) ШчЭМ3ЃЌШє![]() ЃЌЕуEдкADЩЯЃЌ
ЃЌЕуEдкADЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђBDЃН_____
ЃЌдђBDЃН_____
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдквЛПще§ЗНаЮABCDФОАхЩЯвЊЬљШ§жжВЛЭЌЕФЧНжНЃЌе§ЗНаЮEFCGВПЗжЬљAаЭЧНжНЃЌЁїABEВПЗжЬљBаЭЧНжНЃЌЦфгрВПЗжЬљCаЭЧНжНЃЎAаЭЁЂBаЭЁЂCаЭШ§жжЧНжНЕФЕЅМлЗжБ№ЮЊУПЦНЗНУз60дЊЁЂ80дЊЁЂ40дЊЃЎ
ЬНОП1ЃКШчЙћФОАхБпГЄЮЊ1УзЃЌFC=![]() УзЃЌдђвЛПщФОАхгУЧНжНЕФЗбгУаш дЊЃЛ
УзЃЌдђвЛПщФОАхгУЧНжНЕФЗбгУаш дЊЃЛ
ЬНОП2ЃКШчЙћФОАхБпГЄЮЊ2УзЃЌе§ЗНаЮEFCGЕФБпГЄЮЊxУзЃЌвЛПщФОАхашгУЧНжНЕФЗбгУЮЊyдЊЃЌ

ЃЈ1ЃЉгУКЌxЕФДњЪ§ЪНБэЪОyЃЈаДЙ§ГЬЃЉЃЎ
ЃЈ2ЃЉШчЙћвЛПщФОАхашгУЧНжНЕФЗбгУЮЊ225дЊЃЌЧѓе§ЗНаЮEFCGЕФБпГЄЮЊЖрЩйУзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=2x2+bxЉ1ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЮоТлbШЁЪВУДжЕЃЌЖўДЮКЏЪ§y=2x2+bxЉ1ЭМЯѓгыxжсБигаСНИіНЛЕуЃЎ
ЃЈ2ЃЉШєСНЕуPЃЈЉ3ЃЌmЃЉКЭQЃЈ1ЃЌmЃЉдкИУКЏЪ§ЭМЯѓЩЯЃЎ
ЂйЧѓbЁЂmЕФжЕЃЛ
ЂкНЋЖўДЮКЏЪ§ЭМЯѓЯђЩЯЦНвЦЖрЩйЕЅЮЛГЄЖШКѓЃЌЕУЕНЕФКЏЪ§ЭМЯѓгыxжсжЛгавЛИіЙЋЙВЕуЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§![]() гы
гы![]() ЃЈ
ЃЈ![]() ЃЉдкЭЌвЛжБНЧзјБъЯЕжаЕФДѓжТЭМЯѓПЩФмЪЧЃЈ ЃЉ
ЃЉдкЭЌвЛжБНЧзјБъЯЕжаЕФДѓжТЭМЯѓПЩФмЪЧЃЈ ЃЉ
A.  B.
B.  C.
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=Љ![]() ЃЈx+1ЃЉЃЈxЉ3ЃЉгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЮЊИУХзЮяЯпЕФЖдГЦжсЩЯвЛЕуЃЌЕБЕуDЕНжБЯпBCКЭЕНxжсЕФОрРыЯрЕШЪБЃЌдђЕуDЕФзјБъЮЊ ЃЎ
ЃЈx+1ЃЉЃЈxЉ3ЃЉгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЮЊИУХзЮяЯпЕФЖдГЦжсЩЯвЛЕуЃЌЕБЕуDЕНжБЯпBCКЭЕНxжсЕФОрРыЯрЕШЪБЃЌдђЕуDЕФзјБъЮЊ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
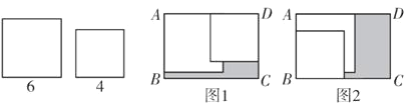
ЁОЬтФПЁПШчЭМЃЌвбжЊдкОиаЮABCDФкЃЌНЋСНеХБпГЄЗжБ№ЮЊ6КЭ4ЕФе§ЗНаЮжНЦЌАДЭМ1ЃЌЭМ2СНжжЗНЪНЗХжУ(ЭМ1ЃЌЭМ2жаСНеХе§ЗНаЮжНЦЌОљгаВПЗжжиЕў)ЃЌОиаЮжаФЉБЛетСНеХе§ЗНаЮжНЦЌИВИЧЕФВПЗжгУвѕгАБэЪОЃЌЩшЭМ1жавѕгАВПЗжЕФУцЛ§ЮЊS1ЃЌЭМ2жавѕгАВПЗжЕФУцЛ§ЮЊS2.ЕБAD-AB=2ЪБЃЌS2-S1ЕФжЕЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=Љx2+bx+cЩЯВПЗжЕуЕФКсзјБъxЃЌзнзјБъyЕФЖдгІжЕШчЯТБэЫљЪОЃК
x | Ё | Љ2 | Љ1 | 0 | 1 | 2 | Ё |
y | Ё | 0 | 4 | 6 | 6 | 4 | Ё |
ДгЩЯБэПЩжЊЃЌЯТСаЫЕЗЈжаЃЌДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
A. ХзЮяЯпгыxжсЕФвЛИіНЛЕузјБъЮЊЃЈЉ2ЃЌ0ЃЉ B. ХзЮяЯпгыyжсЕФНЛЕузјБъЮЊЃЈ0ЃЌ6ЃЉ
C. ХзЮяЯпЕФЖдГЦжсЪЧжБЯпx=0 D. ХзЮяЯпдкЖдГЦжсзѓВрВПЗжЪЧЩЯЩ§ЕФ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com