【题目】函数
与
（
）在同一直角坐标系中的大致图象可能是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】试题分析：由解析式
可得：抛物线对称轴x=0；
A．由双曲线的两支分别位于二、四象限，可得k＜0，则﹣k＞0，抛物线开口方向向上、抛物线与y轴的交点为y轴的负半轴上；本图象与k的取值相矛盾，故A错误；
B．由双曲线的两支分别位于一、三象限，可得k＞0，则﹣k＜0，抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上，本图象符合题意，故B正确；
C．由双曲线的两支分别位于一、三象限，可得k＞0，则﹣k＜0，抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上，本图象与k的取值相矛盾，故C错误；
D．由双曲线的两支分别位于一、三象限，可得k＞0，则﹣k＜0，抛物线开口方向向下、抛物线与y轴的交点在y轴的正半轴上，本图象与k的取值相矛盾，故D错误．
故选B．
科目：初中数学 来源： 题型：
【题目】已知：x1，x2，…x2012都是不等于0的有理数，请你探究以下问题：
（1）若y1=
，则
= ；
（2）若y2=
，则
= ；
（3）若y3=
，则
= ；
（4）由以上探究可知，y2012=
，
共有 个不同的值。请求出这些不同的y2012的值的绝对值的和。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图抛物线
与
轴交于A（1,0），
两点
（1）求该抛物线的解析式；
（2）设（1）中的抛物线交
轴于
点，在该抛物线的对称轴上是否存在点
，使得
的周长最小？若存在，求出点的坐标；若不存在，请说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌
粽子，每盒进价是40元，超市规定每盒售价不得少于45元．根据以往销售经验发现：当售价定为每盒45元时，每天可卖出700盒，每盒售价每提高1元，每天要少卖出20盒．
（1）试求出每天的销售量y（盒）与每盒售价
（元）之间的函数关系式；（4分）
（2）当每盒售价定为多少元时，每天销售的利润
（元）最大？最大利润是多少？（6分）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC 中，BD、CE分别是AC、AB上的高，BD与CE交于点O，BE=CD。
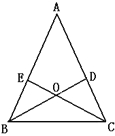
（1）△ABC是等腰三角形吗？为什么？
（2）点O在∠A的平分线上吗？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）
A方法：剪6个侧面； B方法：剪4个侧面和5个底面。
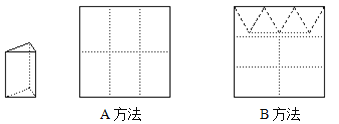
现有38张硬纸板，裁剪时x张用A方法，其余用B方法。
（1）用x的代数式分别表示裁剪出的侧面和底面的个数；
（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，AB= 20cm，BC=16cm，点D为线段AB的中点，动点P以2cm/s的速度从B点出发在射线BC上运动，同时点Q以a cm/s（a＞0且a≠2）的速度从C点出发在线段CA上运动，设运动时间为x秒．
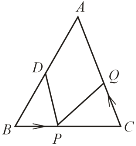
（1）若AB=AC，P在线段BC上，求当a为何值时，能够使△BPD和△CQP全等？
（2）若
，求出发几秒后，
为直角三角形？
（3）若
，当
的度数为多少时，
为等腰三角形？（请直接写出答案，不必写出过程）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】这是一个很著名的故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏？阿基米德对国王说：“我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放十六粒……按这个方法放满整个棋盘就行。”国王以为要不了多少粮食，就随口答应了,结果国王输了．
（1）我们知道,国际象棋共有64个格子,则在第64格中应放多少米？（用幂表示）
（2）请探究第（1）中的数的末位数字是多少?（简要写出探究过程．）
（3）你知道国王输给了阿基米德多少粒米吗?为解决这个问题,我们先来看下面的解题过程：
用分数表示无限循环小数：
．
解：设
①．等式两边同时乘以10,得
②．
将②
①得：
,则
，∴
．
请参照以上解法求出国王输给阿基米德的米粒数（用幂的形式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个三角形的三个外角之比为3：4：5，则这个三角形内角之比是 （ ）．
A. 5：4：3 B. 4：3：2 C. 3：2：1 D. 5：3：1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com