【题目】如图抛物线
与
轴交于A（1,0），
两点
（1）求该抛物线的解析式；
（2）设（1）中的抛物线交
轴于
点，在该抛物线的对称轴上是否存在点
，使得
的周长最小？若存在，求出点的坐标；若不存在，请说明理由。
【答案】（1）y=-x2-2x+3．（2）存在，（-1，2）．
【解析】
试题分析：（1）将点A、点B的坐标代入可求出b、c的值，继而可得出该抛物线的解析式；
（2）连接BC，则BC与对称轴的交点，即是点M的位置，求出直线BC的解析式后，可得出点M的坐标．
试题解析：（1）把A（1，0）、B（-3，0）代入抛物线解析式可得：
，
解得：
故抛物线的解析式为y=-x2-2x+3．
（2）存在．
由题意得，点B与点A关于抛物线的对称轴对称，连接BC，则BC与抛物线对称轴的交点是点M的位置，
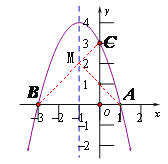
设直线BC解析式为y=kx+b，把B（-3，0）、C（0，3）代入得：
，
解得：
，
则直线BC的解析式为y=x+3，
令MX=-1得My=2，
故点M的坐标为：（-1，2）．
科目：初中数学 来源： 题型：
【题目】某校办工厂生产一批新产品，现有两种销售方案。
方案一：在这学期开学时售出该批产品，可获利30000元，然后将该批产品的成本（生产该批产品支出的总费用）和已获利30000元进行再投资，到这学期结束时，再投资又可获利4.8%；
方案二：这学期结束时售出该批产品，可获利35940元，但要付成本的0.2%作保管费。
（1）设该批产品的成本为x元，方案一的获利为y1元，方案二的获利为y2元，分别求出y1，y2与x的关系式.
（2）当该批产品的成本是多少元时，方案一与方案二的获利是一样的？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：
，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的80%．
（1）设小明每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．
（2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？
（3）如果小明想要每月获得的利润为2000元，那么小明每月的成本需要多少元？（成本＝进价×销售量）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两同学只有一张乒乓球比赛的门票，谁都想去，最后商定通过转盘游戏决定．游戏规则是：转动下面平均分成三个扇形且标有不同颜色的转盘，转盘连续转动两次，若指针前后所指颜色相同，则甲去；否则乙去．（如果指针恰好停在分割线上，那么重转一次，直到指针指向一种颜色为止）
（1）转盘连续转动两次，指针所指颜色共有几种情况？通过画树状图或列表法加以说明；
（2）你认为这个游戏公平吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：
（1）20筐白菜中，最重的一筐比最轻的一筐多重多少千克？
（2）与标准重量比较，20筐白菜总计超过或不足多少千克？
（3）若白菜每千克售价2.6元，则出售这20筐白菜可卖多少元？（结果保留整数）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一个附有进水管、出水管的水池，每单位时间内进出水管的进、出水量都是一定的，设从某时刻开始，4h内只进水不出水，在随后的时间内不进水只出水，得到的时间x（h）与水量y（m3）之间的关系图（如图）．回答下列问题：
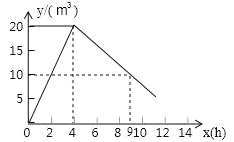
（1）进水管4h共进水多少？每小时进水多少？
（2）当0≤x≤4时，y与x有何关系？
（3）当x=9时，水池中的水量是多少？
（4）若4h后，只放水不进水，那么多少小时可将水池中的水放完？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下图，每个小正方形的边长均为1，可以得到每个小正方形的面积为1．
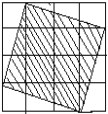
（1）图中阴影部分的面积是多少？ 阴影部分正方形的边长是多少？
（2）估计边长的值在哪两个整数之间？
（3）请你利用图形在数轴上用刻度尺和圆规表示阴影部分正方形边长所表示的数。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD⊥BC，垂足为D．CD=1，AD=2，BD=4．
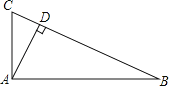
（1）求∠BAC的度数？并说明理由；
（2）P是边BC上一点，连结AP，当△ACP为等腰三角形时，求CP的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
