
【题目】如图,AD⊥BC,垂足为D.CD=1,AD=2,BD=4.
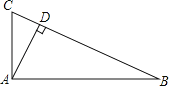
(1)求∠BAC的度数?并说明理由;
(2)P是边BC上一点,连结AP,当△ACP为等腰三角形时,求CP的长.
【答案】(1)∠BAC=90°;(2)CP的长为2或![]() 或2.5.
或2.5.
【解析】
试题分析:首先由勾股定理求出AC和AB,再由勾股定理逆定理证出△ABC为直角三角形得出∠BAC=90°;当△ACP为等腰三角形时,CP有三个解.
解:(1)∠BAC=90°;理由:
∵AD⊥BC,
∴∠ADC=∠ADB=90°;
由勾股定理可得 AC2=AD2+CD2=12+22=5,AB2=AD2+BD2=22+42=20;
∴AC2+AB2=25;
∵BC2=(BD+CD)2=52=25;
∴AC2+AB2=BC2;
∴△ABC是直角三角形;
∴∠BAC=90°;
(2)当△ACP为等腰三角形时,有三种情况:
①当AC=AP时,CP=2CD=2;
②当AC=CP时,∵AC=![]() ,∴CP=
,∴CP=![]() ;
;
③当CP=AP时,CP=![]() =2.5;
=2.5;
因此,当△ACP为等腰三角形时,CP的长为2或![]() 或2.5.
或2.5.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 与
与![]() 轴交于A(1,0),
轴交于A(1,0),![]() 两点
两点

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交![]() 轴于
轴于![]() 点,在该抛物线的对称轴上是否存在点
点,在该抛物线的对称轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出
的周长最小?若存在,求出![]() 点的坐标;若不存在,请说明理由。
点的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
中,AB= 20cm,BC=16cm,点D为线段AB的中点,动点P以2cm/s的速度从B点出发在射线BC上运动,同时点Q以a cm/s(a>0且a≠2)的速度从C点出发在线段CA上运动,设运动时间为x秒.
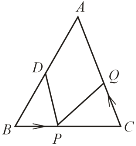
(1)若AB=AC,P在线段BC上,求当a为何值时,能够使△BPD和△CQP全等?
(2)若![]() ,求出发几秒后,
,求出发几秒后,![]() 为直角三角形?
为直角三角形?
(3)若![]() ,当
,当![]() 的度数为多少时,
的度数为多少时,![]() 为等腰三角形?(请直接写出答案,不必写出过程).
为等腰三角形?(请直接写出答案,不必写出过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放十六粒……按这个方法放满整个棋盘就行。”国王以为要不了多少粮食,就随口答应了,结果国王输了.
(1)我们知道,国际象棋共有64个格子,则在第64格中应放多少米?(用幂表示)
(2)请探究第(1)中的数的末位数字是多少?(简要写出探究过程.)
(3)你知道国王输给了阿基米德多少粒米吗?为解决这个问题,我们先来看下面的解题过程:
用分数表示无限循环小数:![]() .
.
解:设![]() ①.等式两边同时乘以10,得
①.等式两边同时乘以10,得![]() ②.
②.
将②![]() ①得:
①得:![]() ,则
,则![]() ,∴
,∴![]() .
.
请参照以上解法求出国王输给阿基米德的米粒数(用幂的形式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信检修小组从A地出发,在东西向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-3 | +7 | -9 | +8 | +6 | -5 | -4 |
(1)求收工时距A地多远?
(2)在第几次纪录时距A地最远?
(3)若每km耗油0.2升,问共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三角形的三个外角之比为3:4:5,则这个三角形内角之比是 ( ).
A. 5:4:3 B. 4:3:2 C. 3:2:1 D. 5:3:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法是真命题的是( )
A.三条直线两两相交,则一共有3个交点
B.垂直于同一条直线的两条直线互相垂直
C.从直线外一点到这条直线的垂线段,是这点到这条直线的距离
D.在平面内过一点有且只有一条直线与已知直线垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com