
【题目】有一个附有进水管、出水管的水池,每单位时间内进出水管的进、出水量都是一定的,设从某时刻开始,4h内只进水不出水,在随后的时间内不进水只出水,得到的时间x(h)与水量y(m3)之间的关系图(如图).回答下列问题:
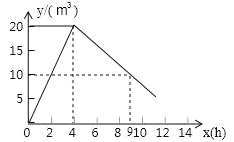
(1)进水管4h共进水多少?每小时进水多少?
(2)当0≤x≤4时,y与x有何关系?
(3)当x=9时,水池中的水量是多少?
(4)若4h后,只放水不进水,那么多少小时可将水池中的水放完?
【答案】(1)进水20m3,所以每小时进水量为5m3.(2)y=5x(0≤x≤4).(3)10m3.(4)10h.
【解析】
试题分析:在本题中横坐标的意义是进出水的时间,纵坐标表示水池中的水量,从图象看0≤x≤4时,y是x的正比例函数;x>4时,y是x的一次函数,根据函数关系解决问题即可.
试题解析:(1)由图象知,4h共进水20m3,所以每小时进水量为5m3.
(2)y是x的正比例函数,设y=kx,由于其图象过点(4,20),所以20=4k,k=5,即y=5x(0≤x≤4).
(3)由图象可知:当x=9时y=10,即水池中的水量为10m3.
(4)由于x≥4时,图象是一条直线,所以y是x的一次函数,
设y=kx+b,由图象可知,该直线过点(4,20),(9,10).
∴![]()
∴![]()
∴y=-2x+28
令y=0,则-2x+28=0,∴x=14.
14-4=10,所以4h后,只放水不进水,10h就可以把水池里的水放完.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】起重机将质量为6.5t的货物沿竖直方向提升了2m,则起重机提升货物所做的功用科学记数法表示为(g=10N/kg)
A.1.3×106J B.13×105JC.13×104J D.1.3×105J
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm) | 10 | 15 | 20 | 25 | 30 |
y(g) | 30 | 20 | 15 | 12 | 10 |
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果品批发公司以16元/千克购进一批樱桃.由往年市场销售情况的统计分析可知:当销售价定为25 元/千克时,每天可售出1 000 千克;若销售价定为20元/千克时,每天可售出2000千克.假设每天的销售量y(千克)与销售价x(元/千克)之间满足一次函数.
(1)试求y与x之间的函数关系式;
(2)在商品无积压且不考虑其他因素的条件下,销售价格定为多少时,才能使每天的销售毛利润W(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 与
与![]() 轴交于A(1,0),
轴交于A(1,0),![]() 两点
两点

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交![]() 轴于
轴于![]() 点,在该抛物线的对称轴上是否存在点
点,在该抛物线的对称轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出
的周长最小?若存在,求出![]() 点的坐标;若不存在,请说明理由。
点的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店积压了100件某种商品,为使这批货物尽快脱手,该商店采取了如下销售方案,将价格提高到原来的2.5倍,再作3次降价处理;第一次降价30%,标出“亏本价”;第二次降价30%,标出“破产价”;第三次降价30%,标出“跳楼价”.3次降价处理销售结果如下表:
降价次数 | 一 | 二 | 三 |
销售件数 | 10 | 40 | 一抢而光 |
(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪种方案更盈利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌
粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价![]() (元)之间的函数关系式;(4分)
(元)之间的函数关系式;(4分)
(2)当每盒售价定为多少元时,每天销售的利润![]() (元)最大?最大利润是多少?(6分)
(元)最大?最大利润是多少?(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
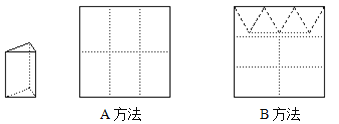
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com