
【题目】如图,△ABC 中,BD、CE分别是AC、AB上的高,BD与CE交于点O,BE=CD。
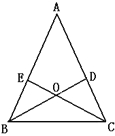
(1)△ABC是等腰三角形吗?为什么?
(2)点O在∠A的平分线上吗?为什么?
【答案】证明见解析.
【解析】
试题分析:(1)先利用HL证明Rt△BCD与Rt△CBE全等,然后根据全等三角形对应角相等可得∠ABC=∠ACB,再根据等角对等边的性质可得AB=AC,所以△ABC是等腰三角形;
(2)根据(1)中Rt△BCD≌Rt△CBE,然后利用全等三角形对应边相等可得BD=CE,对应角相等可得∠BCE=∠CBD,然后利用等角对等边可得BO=CO,相减可得OD=OE,再根据到角的两边距离相等的点在角的平分线上即可证明.
试题解析:(1)△ABC是等腰三角形
理由如下:∵BD、CE是△ABC的高,∴△BCD与△CBE是直角三角形,在Rt△BCD与Rt△CBE中![]() ,∴Rt△BCD≌Rt△CBE(HL),∴∠ABC=∠ACB,∴AB=AC,即△ABC是等腰三角形.
,∴Rt△BCD≌Rt△CBE(HL),∴∠ABC=∠ACB,∴AB=AC,即△ABC是等腰三角形.
(2)点O在∠A的平分线上.
理由如下:∵Rt△BCD≌Rt△CBE,∴BD=CE,∠BCE=∠CBD,∴BO=CO,
∴BD-BO=CE-CO,即OD=OE,∵BD、CE是△ABC的高,
∴点O在∠A的平分线上(到角的两边距离相等的点在角的平分线上).


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】有两个一红一黄大小均匀的小正方体,每个小正方体的各个面上分别标有数字1,2,3,4,5,6.如同时掷出这两个小正方体,将它们朝上的面的数字分别组成一个两位数.(红色数字作为十位,黄色数字作为个位),请回答下列问题.
(1)请分别写出一个必然事件和一个不可能事件.
(2)得到的两位数可能有多少个?其中个位与十位上数字相同的有几个?
(3)任写出一组两个可能性一样大的事件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下图,每个小正方形的边长均为1,可以得到每个小正方形的面积为1.
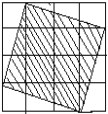
(1)图中阴影部分的面积是多少? 阴影部分正方形的边长是多少?
(2)估计边长的值在哪两个整数之间?
(3)请你利用图形在数轴上用刻度尺和圆规表示阴影部分正方形边长所表示的数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国一些地区遭受旱灾,旱灾牵动全国人民的心.图(1)是我市某中学“献爱心,抗旱灾”自愿捐款活动中学生捐款情况制成的条形统计图,图(2)是该中学学生人数比例分布(已知该校共有学生1450人).
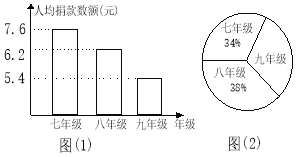
(1)初三学生共捐款多少元?
(2)该校学生平均每人捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点。
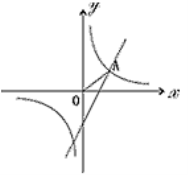
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上, 求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在促销期间规定:商场内所有商品按标价的80%出售,同时当顾客在该商场消费满一定金额后,按如下方案获得相应金额的奖券:
消费金额a(元)范围 | 200≤a<400 | 400≤a<500 | 500≤a<700 | 700≤a<900 | … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在商场内购物可以获得双重优惠。例如,购买标价为450元的商品,则消费金额为![]() 元,获得的优惠额为450×(1-80%)+30=120元,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。
元,获得的优惠额为450×(1-80%)+30=120元,设购买该商品得到的优惠率=购买商品获得的优惠额÷商品的标价。
(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在500元与800元之间(含500元和800元)的商品,顾客购买标价为多少元的商品,可以得到![]() 的优惠率?
的优惠率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com