练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：

    x

    …

    ﹣2

    ﹣1

    0

    1

    2

    …

    y

    …

    0

    4

    6

    6

    4

    …

    从上表可知，下列说法中，错误的是（　　）

    A. 抛物线与x轴的一个交点坐标为（﹣2，0） B. 抛物线与y轴的交点坐标为（0，6）

    C. 抛物线的对称轴是直线x=0 D. 抛物线在对称轴左侧部分是上升的

    【答案】C

    【解析】解：当x=﹣2时，y=0，∴抛物线过（﹣2，0），∴抛物线与x轴的一个交点坐标为（﹣2，0），故A正确；

    当x=0时，y=6，∴抛物线与y轴的交点坐标为（0，6），故B正确；

    当x=0和x=1时，y=6，∴对称轴为x=，故C错误；

    当x＜时，y随x的增大而增大，∴抛物线在对称轴左侧部分是上升的，故D正确；

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y＝x2＋mx＋n经过点A(3，0)、

    B(0，－3)，点P是直线AB上的动点，过点P作x轴的垂线交抛物线于点M，设点P的横

    坐标为t．

    (1)分别求出直线AB和这条抛物线的解析式．

    (2)若点P在第四象限，连接AM、BM，当线段PM最长时，求△ABM的面积．

    (3)是否存在这样的点P，使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请直接写出点P的横坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】操作探究：

    已知在纸面上有一数轴(如图所示)，

    操作一：

    (1)折叠纸面，使表示的点1与1表示的点重合，则2表示的点与___表示的点重合；

    操作二：

    (2)折叠纸面，使1表示的点与3表示的点重合，回答以下问题：

    ①5表示的点与数___表示的点重合；

    ②表示的点与数___表示的点重合

    若数轴上A. B两点之间距离为9,(A在B的左侧)，且A. B两点经折叠后重合，求A. B两点表示的数是多少?

    操作三：

    (3)已知在数轴上点A表示的数是a，点A移动4个单位，此时点A表示的数和a是互为相反数，求a的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法错误的是（ ）

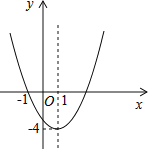
    A．图象关于直线x=1对称

    B．函数y=ax2+bx+c（a≠0）的最小值是﹣4

    C．﹣1和3是方程ax2+bx+c=0（a≠0）的两个根

    D．当x＜1时，y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是由若干个正方体形状的木块堆成的，平放于桌面上。其中，上面正方体的下底面的四个顶点恰是下面相邻正方体的上底面各边的中点，如果最下面的正方体的棱长为1．

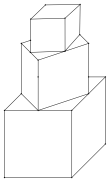
    （1）当只有两个正方体放在一起时，这两个正方体露在外面的面积和是 ；

    （2）当这些正方体露在外面的面积和超过时，那么正方体的个数至少是多少？

    （3）按此规律下去，这些正方体露在外面的面积会不会一直增大？如果会，请说明理由；如果不会，请求出不会超过哪个数值？（提示：所有正方体侧面面积加上所有正方体上面露出的面积之和，就是需求的面积，从简单入手，归纳规律．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一个正五棱柱的底面边长为2cm，高为4cm。

    （1）这个棱柱共有多少个面？计算它的侧面积；

    （2）这个棱柱共有多少个顶点？有多少条棱？

    （3）试用含有的代数式表示棱柱的顶点数、面数、与棱的条数。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】记多项式x2＋2x＋1为 f(x)，多项式y2－4y＋4为f(y)，且多项式f(x)的项数为a，f(y)的次数、一次项系数分别是b、m，数a，b，m数轴上分别对应着点A，B，M．

    （1）求代数式a2－b2的值；

    （2）数轴上有一点G，且到点M，B的距离相等．

    ①求线段GA的长；

    ②若n是关于x的方程mx＋b＝ax的解，且数轴上点N对应着数n，比较线段NG与NB的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个立方体的每个面上都标有数字1、2、3、4、5、6，根据图中该立方体A、B、C三种状态所显示的数字，可推出“？”处的数字是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，A，B两地之间有一座山，汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶，现开通隧道后，汽车直接沿直线AB行驶．已知AC=10km，∠A=30°，∠B=45°，则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果精确到0.1km）（参考数据：≈1.41，≈1.73）

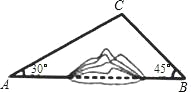
    查看答案和解析>>

    同步练习册答案