
����Ŀ����ͼ�������ɸ���������״��ľ��ѳɵģ�ƽ���������ϡ����У�������������µ�����ĸ�����ǡ������������������ϵ�����ߵ��е㣬������������������ⳤΪ1��
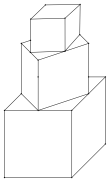
��1����ֻ���������������һ��ʱ��������������¶�������������� ��
��2������Щ������¶�����������ͳ���![]() ʱ����ô������ĸ��������Ƕ��٣�
ʱ����ô������ĸ��������Ƕ��٣�
��3�����˹�����ȥ����Щ������¶�������������һֱ��������ᣬ��˵�����ɣ�������ᣬ��������ᳬ���ĸ���ֵ������ʾ������������������������������������¶�������֮�ͣ����������������Ӽ����֣����ɹ��ɣ���
���𰸡���1��7����2��4������3�����ᣬ���ɼ�����
��������
��1����ֻ��һ�㣨��ֻ��һ����ʱ��ÿ����������1����¶��5���棬������¶���Ϊ��1+1��4=5���������㣬��ڶ���ÿ������������![]() ����һ����ȣ�����4�����棬������¶���Ϊ��1+��1+
����һ����ȣ�����4�����棬������¶���Ϊ��1+��1+![]() ����4=7��
����4=7��
��2���������㣬��������ÿ������������![]() ����������ȣ�����4�����棬������¶���=1+��1+
����������ȣ�����4�����棬������¶���=1+��1+![]() +
+![]() ����4=8����Щ������¶�����������ͳ���8����ô������ĸ���������4����
����4=8����Щ������¶�����������ͳ���8����ô������ĸ���������4����
��3������n�㣬���ԣ�¶����������Ϊ��1+[1+![]() +
+![]() +����+
+����+![]() ]��4��1+2��4=9�������˹��ɶ���ȥ���������ᳬ��9��
]��4��1+2��4=9�������˹��ɶ���ȥ���������ᳬ��9��
�⣺��1����ֻ��һ�㣨��ֻ��һ����ʱ��ÿ����������1����¶��5���棬������¶���Ϊ��1+1��4=5��
�������㣬��ڶ���ÿ������������![]() ����һ����ȣ�����4�����棬������¶���Ϊ��1+��1+
����һ����ȣ�����4�����棬������¶���Ϊ��1+��1+![]() ����4=7��
����4=7��
��3���������㣬��������ÿ������������![]() ����������ȣ�����4�����棬������¶���=1+��1+
����������ȣ�����4�����棬������¶���=1+��1+![]() +
+![]() ����4=8��
����4=8��
����Щ������¶�����������ͳ���8����ô������ĸ���������4����
��3������n�㣬���ԣ�¶����������Ϊ��1+[1+![]() +
+![]() +����+
+����+![]() ]��4��1+2��4=9��
]��4��1+2��4=9��
�ఴ�˹��ɶ���ȥ���������ᳬ��9��


 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=2x2+bx��1��
��1����֤������bȡʲôֵ�����κ���y=2x2+bx��1ͼ����x������������㣮
��2��������P����3��m����Q��1��m���ڸú���ͼ���ϣ�
����b��m��ֵ��
�ڽ����κ���ͼ������ƽ�ƶ��ٵ�λ���Ⱥõ��ĺ���ͼ����x��ֻ��һ�������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �У�
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() �˶����ٶ�Ϊ
�˶����ٶ�Ϊ![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �룬��
�룬��![]() ����
����![]() ������
������![]() ����
����![]() ��Ӧ��Ϊ
��Ӧ��Ϊ![]() ��
��![]() ����ֱ�����
����ֱ�����![]() �����
�����![]() ��
��
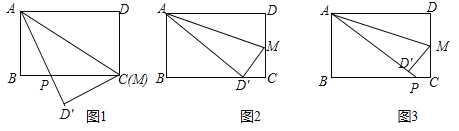
��1����ͼ![]() ����
����![]() ʱ����֤��
ʱ����֤��![]() ��
��
��2����ͼ![]() ����
����![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ǡ�����ڱ�
ǡ�����ڱ�![]() �ϣ�
�ϣ�
��3����ͼ![]() ����
����![]() ʱ����
ʱ����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ���±���
X | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��ۣ�
��ac��0��
�Ƶ�x��1ʱ��y��ֵ��xֵ���������С��
��3�Ƿ���ax2+��b��1��x+c=0��һ������
�ȵ���1��x��3ʱ��ax2+��b��1��x+c��0��
������ȷ�ĸ���Ϊ����
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С������һ���ţ����ż��ӵ��Ľ����������������ߵ�һ����ACB��
���ε�����AE��ED��DB��ɣ���֪�ӵ�ED��ˮƽ�ģ�ED��16m��AE��8m�������ߵĶ���C��ED��
������11m����ED���ڵ�ֱ��Ϊx�ᣬ�����ߵĶԳ���Ϊy�Ὠ��ƽ��ֱ������ϵ��
(1)�������ߵĽ���ʽ��
(2)��֪��ijʱ�̿�ʼ��40h�ڣ�ˮ����ӵ�ED�ľ���h(��λ��m)��ʱ��t(��λ��h)�ı仯���㺯��
��ϵ![]() �ҵ�ˮ�浽����C�ľ��벻����5mʱ�����ֹ��ֻͨ�У���ͨ������˵��������һʱ���ڣ������Сʱ��ֹ��ֻͨ�У�
�ҵ�ˮ�浽����C�ľ��벻����5mʱ�����ֹ��ֻͨ�У���ͨ������˵��������һʱ���ڣ������Сʱ��ֹ��ֻͨ�У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=��x2+bx+c�ϲ��ֵ�ĺ�����x��������y�Ķ�Ӧֵ���±���ʾ��
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | 0 | 4 | 6 | 6 | 4 | �� |
���ϱ���֪������˵���У�������ǣ�������
A. ��������x���һ����������Ϊ����2��0�� B. ��������y��Ľ�������Ϊ��0��6��
C. �����ߵĶԳ�����ֱ��x=0 D. �������ڶԳ�����ಿ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
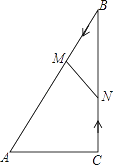
����Ŀ����ͼ����![]() �У�
��![]() ������
������![]() �ӵ�
�ӵ�![]() ������ ��
������ ��![]() ������ÿ��
������ÿ��![]() ���ٶ����
���ٶ����![]() �����˶���ͬʱ����
�����˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ������ÿ��
������ÿ��![]() ���ٶ����
���ٶ����![]() �����˶������˶�ʱ��Ϊ
�����˶������˶�ʱ��Ϊ![]() ��
��![]() ������
������![]() ��
��
![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
![]() ��
��![]() ��
��![]() ���ƣ���
���ƣ���![]() ��ֵ��
��ֵ��
![]() ��
��![]() Ϊ��ֵʱ���ı���
Ϊ��ֵʱ���ı���![]() �����Ϊ
�����Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧϰ�����Ķ����н�����̣�
��һԪ���β���ʽ��x2��5x��0��
�⣺��x2��5x=0����ã�x1=0��x2=5����������y=x2��5x��x��Ľ�������Ϊ��0��0���ͣ�5��0�����������κ���y=x2��5x�Ĵ���ͼ����ͼ��ʾ������ͼ���֪����x��0����x��5ʱ����ͼ��λ��x���Ϸ�����ʱy��0����x2��5x��0�����ԣ�һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ��x��0����x��5��
ͨ��������������̵�ѧϰ����������˼·�ͷ�������������⣺
��1��������������У�����������ѧ˼���е��� ������ ������ֻ����ţ�
��ת��˼�� ����������˼�� �����ν��˼��
��2��һԪ���β���ʽx2��5x��0�Ľ⼯Ϊ�� ��
��3�������Ƶķ�����һԪ���β���ʽ��x2��2x��3��0��
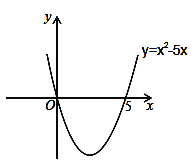
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��B��C��D��E��ͬһֱ��������AC��BD��E���߶�BC���е㣮
![]()
��1����E���߶�AD���е���˵�����ɣ�
��2����AD��10��AB��3ʱ�����߶�BE�ij��ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com