
【题目】如图,矩形OABC摆放在平面直角坐标系![]() 中,点A在
中,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,OA=8,OC=6.
轴上,OA=8,OC=6.
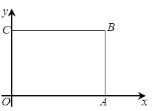

(1)求直线AC的表达式
(2)若直线![]() 与矩形OABC有公共点,求
与矩形OABC有公共点,求![]() 的取值范围;
的取值范围;
(3)若点O与点B位于直线![]() 两侧,直接写出
两侧,直接写出![]() 的取值范围。
的取值范围。
【答案】(1)![]() ;(2)-8<b<6;(3)
;(2)-8<b<6;(3)![]() .
.
【解析】
(1)由条件可先求得A、C两点的坐标,再利用待定系数法可求得直线AC的解析式;
(2)当直线y=x+b过C点和A点时,可求得b的最大值和最小值,可求得b的取值范围;
(3)把点A(0,0),点B(8,6)代入![]() ,求解即可.
,求解即可.
解:(1)∵OA=8,OC=6,
∴A(8,0),C(0,6),
设直线AC解析式为y=kx+m,
把A、C两点坐标代入可得![]() ,
,
解得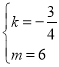 ,
,
∴直线AC的解析式为y=-![]() x+6;
x+6;
(2)由图象可知当直线y=x+b过点C时,把C点坐标代入可得6=0+b,
∴b=6;
当直线y=x+b过点A时,把A点坐标代入可得0=8+b,解得b=-8,
∵若直线y=x+b与矩形OABC有公共点
∴b的取值范围为:-8<b<6,
故答案为: -8<b<6;
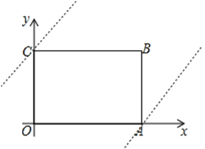
(3)∵OA=8,OC=6,∴B(8,6),
把点A(0,0)代入![]() ,得-2-10k=0,解得:k=-
,得-2-10k=0,解得:k=-![]() ,
,
把点B(8,6)代入![]() ,得8k-2-10k=6 ,解得:k= -4,
,得8k-2-10k=6 ,解得:k= -4,
∴![]() 的取值范围为:
的取值范围为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
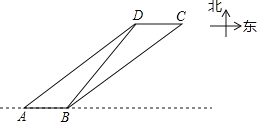
【题目】如图为某海域示意图,其中灯塔D的正东方向有一岛屿C.一艘快艇以每小时20nmile的速度向正东方向航行,到达A处时得灯塔D在东北方向上,继续航行0.3h,到达B处时测得灯塔D在北偏东30°方向上,同时测得岛屿C恰好在B处的东北方向上,此时快艇与岛屿C的距离是多少?(结果精确到1nmile.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中数学 来源: 题型:
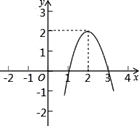
【题目】二次函数![]() 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出方程![]() 的两个根;
的两个根;
(2)写出不等式![]() 的解集;
的解集;
(3)写出![]() 随
随![]() 的增大而增大的自变量
的增大而增大的自变量![]() 的取值范围;
的取值范围;
(4)若方程![]() 没有实数根,求
没有实数根,求![]() 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3a,两动点E,F分别从顶点B,C同时开始以相同速度沿边BC,CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,对应边EG=BC,B,E,C,G在一条直线上.

(1)若BE=a,求DH的长;
(2)当E点在BC边上的什么位置时,△DHE的面积取得最小值?并求该三角形面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
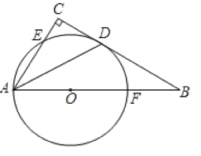
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E. F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求⊙O的半径.
,BF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
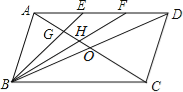
(1)求EG:BG的值;
(2)求证:AG=OG;
(3)设AG=a,GH=b,HO=c,求a:b:c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com