
【题目】如图,正方形ABCD的边长为3a,两动点E,F分别从顶点B,C同时开始以相同速度沿边BC,CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,对应边EG=BC,B,E,C,G在一条直线上.

(1)若BE=a,求DH的长;
(2)当E点在BC边上的什么位置时,△DHE的面积取得最小值?并求该三角形面积的最小值.
【答案】(1)![]() a;(2)E为BC的中点时,
a;(2)E为BC的中点时,![]() a2
a2
【解析】
(1)可通过构建直角三角形求解.连接FH,则FH∥BE且FH=BE,FH⊥CD.因此三角形DFH为直角三角形.
点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,那么DF=3a-a=2a,DF=2a,FH=a,根据勾股定理就求出了DH的长.
(2)设BE=x,△DHE的面积为y,通过三角形DHE的面积=三角形CDE的面积+梯形CDHG的面积-三角形EGH的面积,来得出关于x,y的函数关系式,然后根据函数的性质求出y取最小值时x的值,并求出此时y的值.
解:(1)连接FH,

∵△EGH≌△BCF,
∴HG=FC,∠G=∠BCF,
∴HG∥FC,
∴四边开FCGH是平行四边形,
∴FH∥CG,且FH=CG,
又∵EG=BC,
∴EG-EC=BC-EC,即CG=BE,
∴FH=BE,
∵FH∥CG,
∴∠DFH=∠DCG=90°,
由题意可知:CF=BE=a,
在Rt△DFH中,DF=3a-a=2a,FH=a,
∴DH=![]() =
=![]() a;
a;
(2)设BE=x,△DHE的面积为y,根据题意得:
y=S△CDE+S梯形CDHG-S△EGH=![]() ×3a(3a-x)+
×3a(3a-x)+ ![]() (3a+x)x-
(3a+x)x-![]() ×3a×x,
×3a×x,
∴y=![]() x2-
x2-![]() ax+
ax+![]() a2=
a2=![]() (x-
(x-![]() a)2+
a)2+![]() a2,
a2,
∴当x=![]() a,即E为BC的中点时,y取得最小值,即△DHE的面积取得最小值,最小值是
a,即E为BC的中点时,y取得最小值,即△DHE的面积取得最小值,最小值是![]() a2.
a2.


科目:初中数学 来源: 题型:
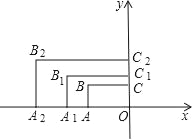
【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是___;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的![]() 倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大![]() 倍,得到矩形A2OC2B,…,按此规律,则矩形A4OC4B4的对称中心的坐标是___.
倍,得到矩形A2OC2B,…,按此规律,则矩形A4OC4B4的对称中心的坐标是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.

(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC摆放在平面直角坐标系![]() 中,点A在
中,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,OA=8,OC=6.
轴上,OA=8,OC=6.
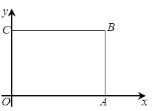

(1)求直线AC的表达式
(2)若直线![]() 与矩形OABC有公共点,求
与矩形OABC有公共点,求![]() 的取值范围;
的取值范围;
(3)若点O与点B位于直线![]() 两侧,直接写出
两侧,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2015年盈利1500万元,到2017年盈利2160万元,且从2015年到2017年,每年盈利的年增长率相同.
(1)求平均年增长率?
(2)若该公司盈利的年增长率继续保持不变,预计2018年盈利多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com