
【题目】如图1,在锐角△ABC中,AB=5,tanC=3,BD⊥AC于点D,BD=3,点P从点A出发,以每秒1个单位长度的速度沿AB向终点B运动,过点P作PE∥AC交边BC于点E,以PE为边作Rt△PEF,使∠EPF=90°,点F在点P的下方,且EF∥AB.设△PEF与△ABD重叠部分图形的面积为S(平方单位)(S>0),点P的运动时间为t(秒)(t>0).
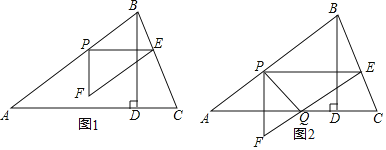
(1)直接写出线段AC的长为 .
(2)当△PEF与△ABD重叠部分图形为四边形时,求S与t之间的函数关系式,并写出t的取值范围.
(3)若边EF所在直线与边AC交于点Q,连结PQ,如图2,
①当PQ将△PEF的面积分成1:2两部分时,求AP的长.
②直接写出△ABC的某一顶点到P、Q两点距离相等时t的值.
【答案】(1)5;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
(3)① ![]() ,
,![]() ; ②
; ②![]() ,
,![]() ,
,![]() .
.
【解析】
(1)在Rt△ABD中,利用勾股定理求出AD.在Rt△BDC中,求出CD即可.
(2)分2种情形求解:如图1中,当0<t≤1时,重叠部分是四边形PMDN.如图2中,当![]() t<5时,重叠部分是四边形PNMF.
t<5时,重叠部分是四边形PNMF.
(3)①分两种情形,分别构建方程即可解决问题;
②分三种情形:如图5中,当PQ的垂直平分线经过当A时.根据PE=PA,可得t=5﹣t解决问题.如图6中,当PQ的垂直平分线经过点B时,作EN⊥AC于N,EP交BD于M.在Rt△BQD中,根据BQ2=QD2+BD2,列出方程即可解决问题.如图7中,当PQ的垂直平分线经过点B时,连接PC,延长PF交AC于G.想办法证明PA=PC即可解决问题.
(1)在Rt△ABD中,∠BDA=90°,AB=5,BD=3,∴AD![]() 4.在Rt△BCD中,∠BDC=90°,BD=3,tanc=3,∴CD
4.在Rt△BCD中,∠BDC=90°,BD=3,tanc=3,∴CD![]() 1,∴AC=AD+CD=4+1=5.
1,∴AC=AD+CD=4+1=5.
(2)①如图1中,当0<t≤1时,重叠部分是四边形PMDN.
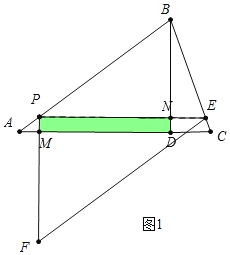
易知PA=t,AM![]() t,PM
t,PM![]() t,DM=4
t,DM=4![]() t,∴S
t,∴S![]() t(4
t(4![]() t)
t)![]() t2
t2![]() t.
t.
②如图2中,当![]() t<5时,重叠部分是四边形PNMF.
t<5时,重叠部分是四边形PNMF.
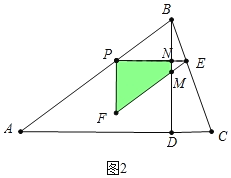
∵AB=5,AC=AD+CD=4+1=5,∴AC=AB,易证PB=PE=5﹣t,PF![]() (5﹣t),PN
(5﹣t),PN![]() (5﹣t),S
(5﹣t),S![]() (5﹣t)
(5﹣t)![]() (5﹣t)
(5﹣t)![]()
![]() (5﹣t)
(5﹣t)![]()
![]() (5﹣t)
(5﹣t)![]() (5﹣t)2.
(5﹣t)2.
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
(3)①如图3中,PF交AC于G.
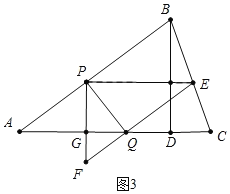
当S△PFQ:S△PEQ=1:2时,∴S△PEQ:S△PEF=2:3,∴![]() PEPG:
PEPG:![]() PEPF=2:3,∴PG:PF=2:3,∴
PEPF=2:3,∴PG:PF=2:3,∴![]() t
t![]() (5﹣t)=2:3,∴t
(5﹣t)=2:3,∴t![]() ,即AP
,即AP![]() .
.
如图4.
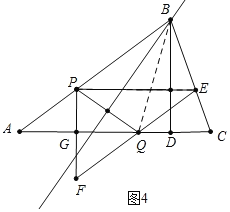
当S△PFQ:S△PEQ=2:1时,∴S△PEQ:S△PEF=1:3,∴![]() PEPG:
PEPG:![]() PEPF=1:3,∴PG:PF=1:3,∴
PEPF=1:3,∴PG:PF=1:3,∴![]() t:
t:![]() (5﹣t)=1:3,∴t
(5﹣t)=1:3,∴t![]() ,即AP
,即AP![]() .
.
综上所述:AP的值为![]() 或
或![]() .
.
②如图5中,当PQ的垂直平分线经过当A时.
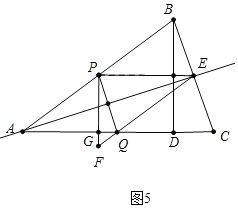
易知四边形APEQ时菱形,∴PE=PA,即t=5﹣t,∴t![]() .
.
如图6中,当PQ的垂直平分线经过点B时,作EN⊥AC于N,EP交BD于M.
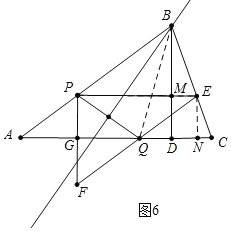
易知四边形PENG时矩形,四边形DMEN时矩形,∴PG=EN![]() t,EM=DN=PE﹣PM
t,EM=DN=PE﹣PM![]() (5﹣t),QN
(5﹣t),QN![]() EN
EN![]() t,∴QD=4﹣(5﹣t)=t﹣1.在Rt△BQD中,∵BQ2=QD2+BD2,∴(5﹣t)2=32+(t﹣1)2,∴/span>t
t,∴QD=4﹣(5﹣t)=t﹣1.在Rt△BQD中,∵BQ2=QD2+BD2,∴(5﹣t)2=32+(t﹣1)2,∴/span>t![]() .
.
如图7中,当PQ的垂直平分线经过点B时,连接PC,延长PF交AC于G.
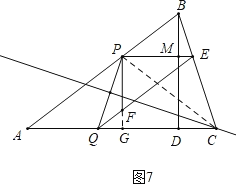
∵PB=PE=5﹣t,PF![]() (5﹣t),PG
(5﹣t),PG![]() t,CG=5
t,CG=5![]() t,∴FG=PG﹣PF
t,∴FG=PG﹣PF![]() t
t![]() (5﹣t)
(5﹣t)![]() t
t![]() ,∴GQ
,∴GQ![]() FG
FG![]() t﹣5,∴CP=CQ=GQ+CG
t﹣5,∴CP=CQ=GQ+CG![]() t﹣5+5
t﹣5+5![]() t=t,∴PA=PC.
t=t,∴PA=PC.
∵PG⊥AC,∴AG=CG![]() ,∴t=PA
,∴t=PA![]() AG
AG![]() .
.
综上所述:t![]() s或
s或![]() s或
s或![]() s时,PQ的垂直平分线经过△ABC的顶点.
s时,PQ的垂直平分线经过△ABC的顶点.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
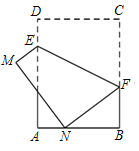
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E,F分别为边AD,BC上的一个动点,连接EF,以EF为对称轴折叠四边形CDEF,得到四边形MNFE,点D,C的对应点分别为M,N,当点N恰好落在AB的三等分点时,CF的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长度等于_____;
(Ⅱ)在图中有一点P,若连接AP,PB,PC,满足AP平分∠A,且PC=PB,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
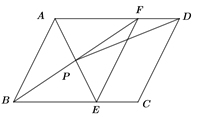
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求PD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO为矩形,点A在x轴上,点C在y轴上,且点B的坐标为(-1,2),将此矩形绕点O顺时针旋转90°得矩形DEFO,抛物线y=-x2+bx+c过B,E两点.
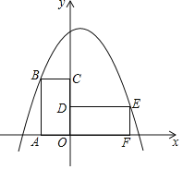
(1)求此抛物线的函数关系式;
(2)将矩形ABCO向上平移,并且使此抛物线平分线段BC,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利44元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出5件。若商场平均每天要盈利1600元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销一种商品,每件成本为20元.经市场调查发现,在一段时间内,销售量w(件)随销售单价x(元/件)的变化而变化,具体关系式为:w=-10x+500.设这种商品在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的函数关系式;
(2)当x取何值时,利润最大?最大利润为多少元?
(3)如果物价部门规定这种商品的销售单价不得高于32元/件,公司想要在这段时间内获得2000元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1=k1x+b与反比例函数![]() 的图象交于A,B两点(点A在点B左侧),已知点A的坐标是(6,2)点B的纵坐标是﹣3.
的图象交于A,B两点(点A在点B左侧),已知点A的坐标是(6,2)点B的纵坐标是﹣3.

(1)求反比例函数和直线l1的表达式;
(2)根据图象直接写出k1x+b>![]() 的解集;
的解集;
(3)将直线l1:![]() 沿y轴向上平移后的直线l2与反比例函数
沿y轴向上平移后的直线l2与反比例函数![]() 在第一象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第一象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
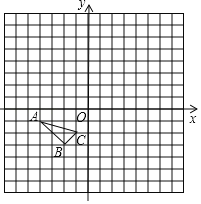
【题目】如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形).图中△ABC是格点三角形,点A,B,C的坐标分别是(﹣4,﹣1),(﹣2,﹣3),(﹣1,﹣2).
(1)以O为旋转中心,把△ABC绕O点顺时针旋转90°后得到△A1B1C1,画出△A1B1C1;
(2)以O为位似中心,在第一象限内把△ABC放大2倍后得到△A2B2C2,画出△A2B2C2;
(3)△ABC内有一点P(a,b),写出经过(2)位似变换后P的对应点P1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com