
【题目】如图,在每个小正方形边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长度等于_____;
(Ⅱ)在图中有一点P,若连接AP,PB,PC,满足AP平分∠A,且PC=PB,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_____.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
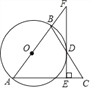
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,DE⊥AC,垂足为E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若∠C=60°,AC=12,求![]() 的长.
的长.
(3)若tanC=2,AE=8,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂每天生产![]() 、
、![]() 两种品牌的服装共600件,
两种品牌的服装共600件,![]() 、
、![]() 两种品牌的服装每件的成本和利润如右表:
两种品牌的服装每件的成本和利润如右表:
A | B | |
成本(元/件) | 50 | 35 |
利润(元/件) | 20 | 15 |
设每天生产![]() 种品牌服装
种品牌服装![]() 件,每天两种服装获利
件,每天两种服装获利![]() 元.
元.
(1)请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,C点表示数c,且a、c满足|a+3|+(c﹣9)2=0.若点A与点B之间的距离表示为AB=|a﹣b|,点B与点C之间的距离表示为BC=|b﹣c|,点B在点A、C之间,且满足BC=2AB.
(1)a= ,b= ,c= ;
(2)若点P为数轴上一动点,其对应的数为x,当代数式|x﹣a|+|x﹣b|+|x﹣c|取得最小值时,此时x= ,最小值为 .
(3)动点M从A点位置出发,沿数轴以每秒1个单位的速度向终点C运动,设运动时间为t秒,当点M运动到B点时,点N从A点出发,以每秒2个单位的速度沿数轴向C点运动,N点到达C点后,再立即以同样的速度返回,运动到终点A.问:在点N开始运动后,M、N两点之间的距离能否为2个单位?如果能,请求出运动的时间t的值以及此时对应的M点所表示的数:如果不能,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来.
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
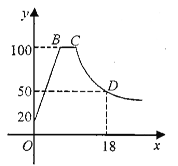
【题目】喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度 y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
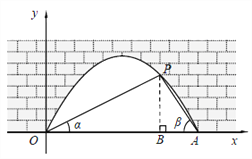
【题目】如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
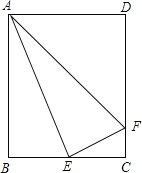
【题目】如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设![]() =k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com