
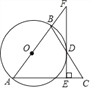
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,DE⊥AC,垂足为E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若∠C=60°,AC=12,求![]() 的长.
的长.
(3)若tanC=2,AE=8,求BF的长.
【答案】(1)见解析;(2) 2π;(3)![]() .
.
【解析】分析:(1)连接OD,根据等腰三角形的性质:等边对等角,得∠ABC=∠C,∠ABC=∠ODB,从而得到∠C=∠ODB ,根据同位角相等,两直线平行,得到OD∥AC,从而得证OD⊥EF,即 EF是⊙O的切线;
(2) 根据中点的性质,由AB=AC=12 ,求得OB=OD=![]() =6,进而根据等边三角形的判定得到△OBD是等边三角形,即∠BOD=600,从而根据弧长公式七届即可;
=6,进而根据等边三角形的判定得到△OBD是等边三角形,即∠BOD=600,从而根据弧长公式七届即可;
(3)连接AD ,根据直角三角形的性质,由在Rt△DEC中, ![]() 设CE=x,则DE=2x,然后由Rt△ADE中,
设CE=x,则DE=2x,然后由Rt△ADE中, ![]() ,求得DE、CE的长,然后根据相似三角形的判定与性质求解即可.
,求得DE、CE的长,然后根据相似三角形的判定与性质求解即可.
详解:(1)连接OD ∵AB=AC ∴∠ABC=∠C
∵OD=OB ∴∠ABC=∠ODB
∴∠C=∠ODB ∴OD∥AC
又∵DE⊥AC ∴OD⊥DE,即OD⊥EF
∴EF是⊙O的切线
(2) ∵AB=AC=12 ∴OB=OD=![]() =6
=6
由(1)得:∠C=∠ODB=600
∴△OBD是等边三角形 ∴∠BOD=600
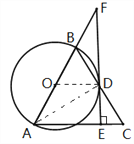
∴![]() =
=![]() 即
即![]() 的长
的长![]()
(3)连接AD ∵DE⊥AC ∠DEC=∠DEA=900
在Rt△DEC中, ![]() 设CE=x,则DE=2x
设CE=x,则DE=2x
∵AB是直径 ∴∠ADB=∠ADC=900
∴∠ADE+∠CDE=900 在Rt△DEC中,∠C+∠CDE=900
∴∠C=∠ADE 在Rt△ADE中, ![]()
∵ AE=8,∴DE=4 则CE=2
∴AC=AE+CE=10 即直径AB=AC=10 则OD=OB=5
∵OD//AE ∴△ODF∽△AEF
∴ ![]() 即:
即:![]()
解得:BF=![]() 即BF的长为
即BF的长为![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
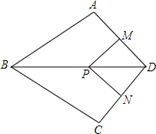
(1)求证:ADB=CDB;
(2)若ADC=90°,求证:四边形MPND是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①若|a|=﹣b,|b|=b,则a=b=0;②若﹣a不是正数,则a为非负数;③|﹣a2|=(﹣a)2;④若![]() ,则
,则![]() ;⑤平面内n条直线两两相交,最多
;⑤平面内n条直线两两相交,最多![]() 个交点.其中正确的结论有( )
个交点.其中正确的结论有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )
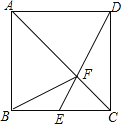
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
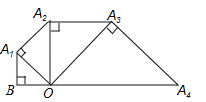
【题目】如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点.
的中点.
![]()
(1)若![]() ,求线段
,求线段![]() 的长度.
的长度.
(2)当线段![]() 在线段
在线段![]() 上从左向右或从右向左运动时,试判断线段
上从左向右或从右向左运动时,试判断线段![]() 的长度是否发生变化,如果不变,请求出线段
的长度是否发生变化,如果不变,请求出线段![]() 的长度;如果变化,请说明理由.
的长度;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长度等于_____;
(Ⅱ)在图中有一点P,若连接AP,PB,PC,满足AP平分∠A,且PC=PB,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com