
【题目】某服装厂每天生产![]() 、
、![]() 两种品牌的服装共600件,
两种品牌的服装共600件,![]() 、
、![]() 两种品牌的服装每件的成本和利润如右表:
两种品牌的服装每件的成本和利润如右表:
A | B | |
成本(元/件) | 50 | 35 |
利润(元/件) | 20 | 15 |
设每天生产![]() 种品牌服装
种品牌服装![]() 件,每天两种服装获利
件,每天两种服装获利![]() 元.
元.
(1)请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )
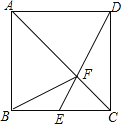
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点.
的中点.
![]()
(1)若![]() ,求线段
,求线段![]() 的长度.
的长度.
(2)当线段![]() 在线段
在线段![]() 上从左向右或从右向左运动时,试判断线段
上从左向右或从右向左运动时,试判断线段![]() 的长度是否发生变化,如果不变,请求出线段
的长度是否发生变化,如果不变,请求出线段![]() 的长度;如果变化,请说明理由.
的长度;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=2![]() ,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若a+b=ab,则称a、b是“相伴数”,例如:3+1.5=3×1.5,因此3和1.5是一组“相伴数”
(1)﹣1与 是一组“相伴数”;
(2)若m、n是一组“相伴数”,2mn﹣![]() [3m+2(
[3m+2(![]() n﹣m)+3mn﹣6]的值.
n﹣m)+3mn﹣6]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
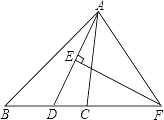
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长度等于_____;
(Ⅱ)在图中有一点P,若连接AP,PB,PC,满足AP平分∠A,且PC=PB,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板的两个锐角顶点重合,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的平分线.
的平分线.
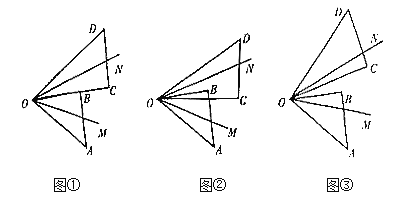
(1)如图①所示,当![]() 与
与![]() 重合时,则
重合时,则![]() 的大小为______.
的大小为______.
(2)当![]() 绕着点
绕着点![]() 旋转至如图②所示,当
旋转至如图②所示,当![]() ,则
,则![]() 的大小为多少?
的大小为多少?
(3)当![]() 绕着点
绕着点![]() 旋转至如图③所示,当
旋转至如图③所示,当![]() 时,求
时,求![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com