
【题目】将一副三角板的两个锐角顶点重合,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的平分线.
的平分线.
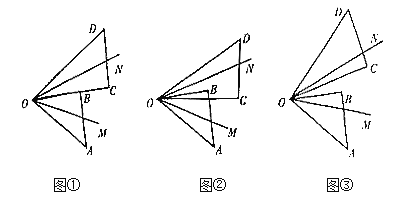
(1)如图①所示,当![]() 与
与![]() 重合时,则
重合时,则![]() 的大小为______.
的大小为______.
(2)当![]() 绕着点
绕着点![]() 旋转至如图②所示,当
旋转至如图②所示,当![]() ,则
,则![]() 的大小为多少?
的大小为多少?
(3)当![]() 绕着点
绕着点![]() 旋转至如图③所示,当
旋转至如图③所示,当![]() 时,求
时,求![]() 的大小.
的大小.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据角平分线的定义可以求得∠MON![]() ∠AOB+
∠AOB+![]() ∠COD=∠BON+∠MOB,即可得出结论;
∠COD=∠BON+∠MOB,即可得出结论;
(2)根据图形可以求得:∠AOC、∠BOD.根据角平分线的定义得到∠BON![]() ∠BOD,∠COM
∠BOD,∠COM![]() ∠AOC,根据∠MON=∠MOC+∠BON+∠BOC即可得到结论;
∠AOC,根据∠MON=∠MOC+∠BON+∠BOC即可得到结论;
(3)根据图形求得∠AOC=45°+n°,∠BOD=30°+n°,根据角平分线的定义得到∠BON=![]() ∠BOD,∠MOB=
∠BOD,∠MOB=![]() ∠AOC-∠BOC,根据∠MON=∠MOB+∠BON即可得到结论.
∠AOC-∠BOC,根据∠MON=∠MOB+∠BON即可得到结论.
(1)∵∠AOB=45°,∠COD=30°,OM,ON分别是∠AOC,∠BOD的角平分线,
∴∠BON![]() ∠COD=15°,∠MOB
∠COD=15°,∠MOB![]() ∠AOB=22.5°,
∠AOB=22.5°,
∴∠MON=37.5°.
故答案为:37.5°;
(2)∠BOC=10°时,∠AOC=35°,∠BOD=20°,
∠BON=![]() ∠BOD=10°,∠MOC=
∠BOD=10°,∠MOC=![]() ∠AOC=17.5°,
∠AOC=17.5°,
∠MON=∠MOC+∠BON+∠BOC=17.5°+10°+10°=37.5°
(3)∠BOC=n°时,∠AOC=45°+n°,∠BOD=30°+n°,
∠BON=![]() ∠BOD=
∠BOD=![]() (30°+n°)=15°+
(30°+n°)=15°+![]() n°
n°
∠MOB=![]() ∠AOC-∠BOC=
∠AOC-∠BOC=![]() (45°+n°)-n°=22.5°-
(45°+n°)-n°=22.5°-![]() n°
n°
∠MON=∠MOB+∠BON=15°+![]() n°+22.5°-
n°+22.5°-![]() n°=37.5°.
n°=37.5°.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】某服装厂每天生产![]() 、
、![]() 两种品牌的服装共600件,
两种品牌的服装共600件,![]() 、
、![]() 两种品牌的服装每件的成本和利润如右表:
两种品牌的服装每件的成本和利润如右表:
A | B | |
成本(元/件) | 50 | 35 |
利润(元/件) | 20 | 15 |
设每天生产![]() 种品牌服装
种品牌服装![]() 件,每天两种服装获利
件,每天两种服装获利![]() 元.
元.
(1)请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
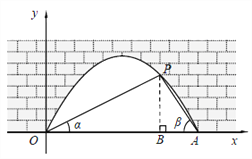
【题目】如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点燃蜡烛,按照与时间成正比例关系变短,长21cm的蜡烛,已知点燃6分钟后,蜡烛变短3.6cm,设蜡烛点燃x分钟后变短ycm,求:
(1)用x表示函数y的解析式;
(2)自变量的取值范围;
(3)此蜡烛几分钟燃烧完?
(4)画出此函数的图像。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:课本上有这样一道例题:“解方程:![]()
解:去分母得:
6(x+15)=15-10(x-7)①
6x+90=15-10x+70②
16x=-5③
x=-![]() ④
④
请回答下列问题:
(1)得到①式的依据是________;
(2)得到②式的依据是________;
(3)得到③式的依据是________;
(4)得到④式的依据是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
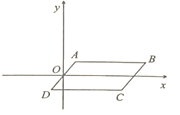
【题目】如图,在平面直角坐标系中,![]() ,顶点
,顶点![]() ;直线
;直线![]() .
.
(1)点![]() 的坐标是______,对角线
的坐标是______,对角线![]() 与
与![]() 的交点
的交点![]() 的坐标是______.
的坐标是______.
(2)①过点![]() 的直线
的直线![]() 的解析式是______.
的解析式是______.
②过点![]() 的直线
的直线![]() 的解析式是______.
的解析式是______.
③判断①、②中两条直线的位置关系是______.
(3)当直线![]() 平分
平分![]() 的面积时,
的面积时,![]() 的值是______.
的值是______.
(4)一次函数![]() 的图像______(填“能”或“不能”)平分
的图像______(填“能”或“不能”)平分![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
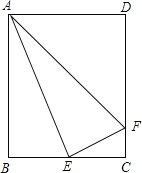
【题目】如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设![]() =k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线![]() 上点
上点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将直角
,将直角![]() 的直角顶点放在点
的直角顶点放在点![]() 处.
处.
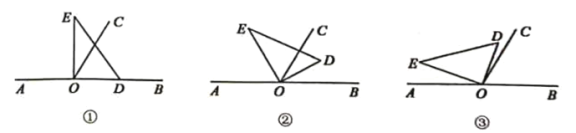
(1)若直角![]() 的边
的边![]() 在射线
在射线![]() 上(图①),求
上(图①),求![]() 的度数;
的度数;
(2)将直角![]() 绕点
绕点![]() 按逆时针方向转动,使得
按逆时针方向转动,使得![]() 所在射线平分
所在射线平分![]() (图②),说明
(图②),说明![]() 所在射线是
所在射线是![]() 的平分线;
的平分线;
(3)将直角![]() 绕点
绕点![]() 按逆时针方向转动到某个位置时,恰好使得
按逆时针方向转动到某个位置时,恰好使得![]() (图③),求
(图③),求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
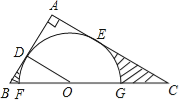
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com