
【题目】如图,在平面直角坐标系中,![]() ,顶点
,顶点![]() ;直线
;直线![]() .
.
(1)点![]() 的坐标是______,对角线
的坐标是______,对角线![]() 与
与![]() 的交点
的交点![]() 的坐标是______.
的坐标是______.
(2)①过点![]() 的直线
的直线![]() 的解析式是______.
的解析式是______.
②过点![]() 的直线
的直线![]() 的解析式是______.
的解析式是______.
③判断①、②中两条直线的位置关系是______.
(3)当直线![]() 平分
平分![]() 的面积时,
的面积时,![]() 的值是______.
的值是______.
(4)一次函数![]() 的图像______(填“能”或“不能”)平分
的图像______(填“能”或“不能”)平分![]() 的面积.
的面积.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ; ③相交;(3)4; (4)不能.
; ③相交;(3)4; (4)不能.
【解析】
(1)根据平行四边形的性质以及A、B两点的坐标可得CD∥AB∥x轴,CD=AB=4,再利用平移的性质得出点C的坐标;根据平行四边形的对角线互相平分得出E是BD的中点,再利用线段的中点坐标公式求出点E的坐标;
(2)①将点A(1,1)代入y=kx-3k+4,求出k的值即可;
②将点B(5,1)代入y=kx-3k+4,求出k的值即可;
③将两直线的解析式联立组成方程组: ,解得:
,解得:![]() ,即可判断①、②中两条直线的位置关系是相交;
,即可判断①、②中两条直线的位置关系是相交;
(3)当直线y=kx-3k+4平分ABCD的面积时,直线y=kx-3k+4经过ABCD对角线的交点E(2,0),将E点坐标代入y=kx-3k+4,求出k的值即可;
(4)将x=2代入y=kx-2k+1,求出y=1≠0,即直线y=kx-2k+1不经过ABCD对角线的交点E(2,0),即可判断一次函数y=kx-2k+1的图象不能平分ABCD的面积.
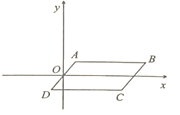
解:(1)∵四边形ABCD是平行四边形,A(1,1),B(5,1),
∴CD∥AB∥x轴,CD=AB=4,
∵D(-1,-1),
∴点C的坐标是(-1+4,-1),即(3,-1),
∵E是对角线AC与BD的交点,
∴E是BD的中点,
∵B(5,1),D(-1,-1),
∴点E的坐标是(2,0).
故答案为(3,-1),(2,0);
(2)①将点A(1,1)代入y=kx-3k+4,
得1=k-3k+4,解得![]() ,
,
则所求的解析式是![]() .
.
故答案为:![]() ;
;
②将点B(5,1)代入y=kx-3k+4,
得1=k-3k+4,解得![]() ,
,
则所求的解析式是![]() ;
;
故答案为:![]() ;
;
③由 ,解得
,解得![]()
∴①、②中两条直线的位置关系是相交,交点是(3,4).
故答案为:相交;
(3)∵直线y=kx-3k+4平分ABCD的面积时,
∴直线y=kx-3k+4经过ABCD对角线的交点E(2,0),
∴0=2k-3k+4,解得k=4.
故答案为:4;
(4)∵x=2时,y=kx-2k+1=1≠0,
∴直线y=kx-2k+1不经过ABCD对角线的交点E(2,0),∴一次函数y=kx-2k+1的图象不能平分ABCD的面积.
故答案为:不能.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
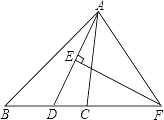
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
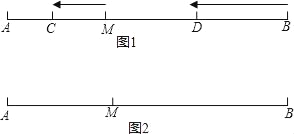
【题目】如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示.
(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.
(2)若点C、D运动时,总有MD=3AC,则:AM= AB.
(3)如图②,若AM=![]() AB,点N是直线AB上一点,且AN﹣BN=MN,求
AB,点N是直线AB上一点,且AN﹣BN=MN,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板的两个锐角顶点重合,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的平分线.
的平分线.
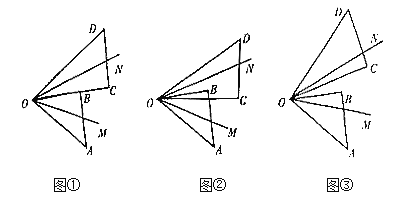
(1)如图①所示,当![]() 与
与![]() 重合时,则
重合时,则![]() 的大小为______.
的大小为______.
(2)当![]() 绕着点
绕着点![]() 旋转至如图②所示,当
旋转至如图②所示,当![]() ,则
,则![]() 的大小为多少?
的大小为多少?
(3)当![]() 绕着点
绕着点![]() 旋转至如图③所示,当
旋转至如图③所示,当![]() 时,求
时,求![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?
时间x(天) | 1≤x<9 | 9≤x<15 | x≥15 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 | |
销量(斤) | 80﹣3x | 120﹣x | |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 | |
(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司有甲、乙、丙三个机器人分配快件,甲单独完成需要x小时,乙单独完成需要y小时,丙单独完成需要z小时.
(1)求甲单独完成的时间是乙丙合作完成时间的几倍?
(2)若甲单独完成的时间是乙丙合作完成时间的a倍,乙单独完成的时间是甲丙合作完成时间的b倍,丙单独完成的时间是甲乙合作完成时间的c倍,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )
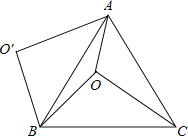
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com