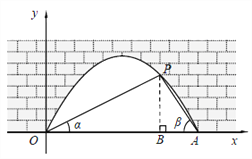
【题目】如图中是抛物线形拱桥，P处有一照明灯，水面OA宽4m，从O、A两处观测P处，仰角分别为α、β，且tanα=
，tanβ=
，以O为原点，OA所在直线为x轴建立直角坐标系.若水面上升1m，水面宽为（ ）
A. 
B. 
C. 
D. 
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，已知线段
，
，点
是
的中点，点
是
的中点.
（1）若
，求线段
的长度.
（2）当线段
在线段
上从左向右或从右向左运动时，试判断线段的长度是否发生变化，如果不变，请求出线段的长度；如果变化，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在每个小正方形边长为1的网格中，点A，B，C均在格点上．
（Ⅰ）AC的长度等于_____；
（Ⅱ）在图中有一点P，若连接AP，PB，PC，满足AP平分∠A，且PC=PB，请在如图所示的网格中，用无刻度的直尺，画出点P，并简要说明点P的位置是如何找到的（不要求证明）_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料，并回答问题
钟表中蕴含着有趣的数学运算，不用负数也可以作减法，例如现在是10点钟，4小时以后是几点钟？虽然
，但在表盘上看到的是2点钟.如果用符号“⊕”表示钟表上的加法，则
.若问2点钟之前4小时是几点钟，就得到钟表上的减法概念，，用符号“”表示钟表上的减法.（注：我们用0点钟代替12点钟）由上述材料可知：
（1）
______，
______；
（2）在有理数运算中，相加得零的两个数互为相反数，如果在钟表运算中沿用这个概念，则5的相反数是______，举例说明有理数减法法则：减去一个数等于加上这个数的相反数，在钟表运算中是否仍然成立；
（3）规定在钟表运算中也有
，对于钟表上的任意数字
，
，
，若
，判断
是否一定成立，若一定成立，说明理由；若不一定成立，写出一组反例，并结合反例加以说明.
查看答案和解析>>
科目：初中数学 来源： 题型：
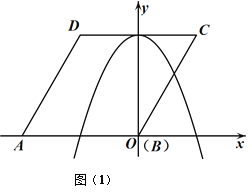
【题目】如图(1)，已知菱形
的边长为
，点
在
轴负半轴上，点
在坐标原点，点
的坐标为（
，
），抛物线
顶点在
边上，并经过
边的中点．
（1）求这条抛物线的函数解析式；
（2）点
关于直线
的对称点是
，求点到点的最短距离；
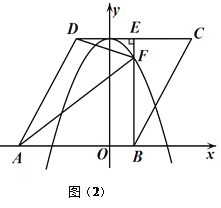
（3）如图（2）将菱形以每秒
个单位长度的速度沿
轴正方向匀速平移，过点作
于点
，交抛物线于点
，连接
、
．设菱形
平移的时间为
秒（
），问是否存在这样的，使
与
相似？若存在，求出
的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一副三角板的两个锐角顶点重合，
，
，
，
分别是
，
的平分线.
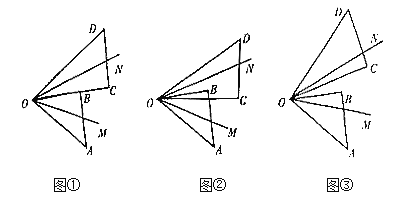
（1）如图①所示，当
与
重合时，则
的大小为______.
（2）当
绕着点
旋转至如图②所示，当
，则的大小为多少？
（3）当绕着点旋转至如图③所示，当
时，求的大小.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点
在数轴上对应的数为
，点
对应的数为
，且
G为线段
上一点，
两点分别从
点沿
方向同时运动，设
点的运动速度为
点的运动速度为
，运动时间为
.
（1）点对应的数为 ，点对应的数为 ；
（2）若
，试求
为多少
时，两点的距离为
；
（3）若
，点
为数轴上任意一点，且
，请直接写出
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
