
【题目】如图,已知AB⊥AC,AD⊥AE,AB=AC,AD=AE,
求证:(1)BE=DC
(2)BE⊥DC。
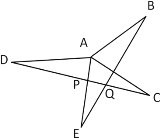
【答案】(1)见解析;(2)见解析.
【解析】
(1)由AB⊥AC,AD⊥AE,且AB=AC,AD=AE,利用SAS可判定△DAC≌△EAB,继而可证得BE=DC;
(2)由△DAC≌△EAB,可得∠ADC=∠AEB,然后根据∠ADC+∠APD=90°,通过等量代换可证得∠EQP=90°,问题得解.
证明:(1)∵AB⊥AC,AD⊥AE,
∴∠BAC=∠EAD=90°,
∴∠DAC=∠EAB,
在△DAC和△EAB中,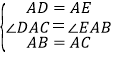 ,
,
∴△DAC≌△EAB(SAS),
∴BE=DC;
(2)∵△DAC≌△EAB,
∴∠ADC=∠AEB,
∵∠ADC+∠APD=90°,∠APD=∠EPQ,
∴∠AEB+∠EPQ=90°,
∴∠EQP=90°,
即BE⊥DC.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂每天生产![]() 、
、![]() 两种品牌的服装共600件,
两种品牌的服装共600件,![]() 、
、![]() 两种品牌的服装每件的成本和利润如右表:
两种品牌的服装每件的成本和利润如右表:
A | B | |
成本(元/件) | 50 | 35 |
利润(元/件) | 20 | 15 |
设每天生产![]() 种品牌服装
种品牌服装![]() 件,每天两种服装获利
件,每天两种服装获利![]() 元.
元.
(1)请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来.
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
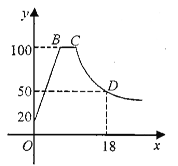
【题目】喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度 y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鞋号是指鞋子的大小,中国于60年代后期,在全国测量脚长的基础上制定了“中国鞋号”,1998年政府发布了基于![]() 系统,用毫米做单位的中华人民共和国国家标准
系统,用毫米做单位的中华人民共和国国家标准![]() ,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:
,被称为“新鞋号”,之前以厘米为单位的鞋号从此被称为“旧鞋号”.新旧鞋号部分对应表如下:
新鞋号 | 220 | 225 | 230 | 235 | … | 270 |
旧鞋号 | 34 | 35 | 36 | 37 | … |
|
(1)![]() 的值为______;
的值为______;
(2)若新鞋号为![]() ,旧鞋号为
,旧鞋号为![]() ,则把旧鞋号转换为新鞋号的公式为______
,则把旧鞋号转换为新鞋号的公式为______
查看答案和解析>>
科目:初中数学 来源: 题型:
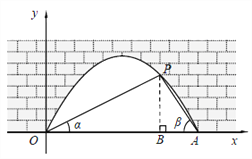
【题目】如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点燃蜡烛,按照与时间成正比例关系变短,长21cm的蜡烛,已知点燃6分钟后,蜡烛变短3.6cm,设蜡烛点燃x分钟后变短ycm,求:
(1)用x表示函数y的解析式;
(2)自变量的取值范围;
(3)此蜡烛几分钟燃烧完?
(4)画出此函数的图像。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线![]() 上点
上点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将直角
,将直角![]() 的直角顶点放在点
的直角顶点放在点![]() 处.
处.
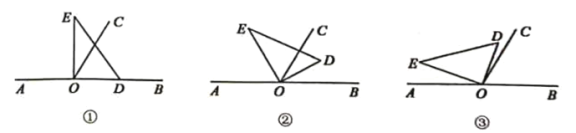
(1)若直角![]() 的边
的边![]() 在射线
在射线![]() 上(图①),求
上(图①),求![]() 的度数;
的度数;
(2)将直角![]() 绕点
绕点![]() 按逆时针方向转动,使得
按逆时针方向转动,使得![]() 所在射线平分
所在射线平分![]() (图②),说明
(图②),说明![]() 所在射线是
所在射线是![]() 的平分线;
的平分线;
(3)将直角![]() 绕点
绕点![]() 按逆时针方向转动到某个位置时,恰好使得
按逆时针方向转动到某个位置时,恰好使得![]() (图③),求
(图③),求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com