
【题目】解不等式组![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来.
![]()
(Ⅳ)原不等式组的解集为 .
科目:初中数学 来源: 题型:
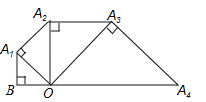
【题目】如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=2![]() ,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
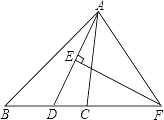
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)AC的长度等于_____;
(Ⅱ)在图中有一点P,若连接AP,PB,PC,满足AP平分∠A,且PC=PB,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照下列要求完成画图及相应的问题解答
(1)画直线![]() ;
;
(2)画![]() ;
;
(3)画线段![]() ;
;
(4)过![]() 点画直线
点画直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() ;
;
(5)请测量点![]() 到直线
到直线![]() 的距离为__________
的距离为__________![]() (精确到0.1
(精确到0.1 ![]() ) .
) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司有甲、乙、丙三个机器人分配快件,甲单独完成需要x小时,乙单独完成需要y小时,丙单独完成需要z小时.
(1)求甲单独完成的时间是乙丙合作完成时间的几倍?
(2)若甲单独完成的时间是乙丙合作完成时间的a倍,乙单独完成的时间是甲丙合作完成时间的b倍,丙单独完成的时间是甲乙合作完成时间的c倍,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com