
����Ŀ�����̲�ǰ��Ҫ��ˮ���ݲ�����������Ҫ������ˮ���е�ˮ�յ�100����Ȼ��ֹͣ��ˮ����ˮ�½��͵��ʺϵ��¶�ʱ���ݲ裬��ˮʱˮ��y��������ʱ��x��min����һ�κ�����ϵ��ֹͣ���ȹ���1���Ӻ�ˮ����ˮ���¶� y��������ʱ��x��min�������ڷ�����������ϵ����ͼ������֪ˮ����ˮ�ij�ʼ�¶���20�������¹�����ˮ�²�����20����
��1���ֱ����ͼ������Ӧ�ĺ�����ϵʽ������д���Ա���x��ȡֵ��Χ��
��2����ˮ���е�ˮ�տ���100��������80���Ϳ��Խ��������̲裬�ʴ�ˮ�տ����ݲ���Ҫ�ȴ��ʱ�䣿
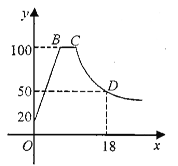
���𰸡���1����������ˮ��������ϵʽΪy=10x+20��0��x��8����
��ֹͣ���ȣ���y��x�ĺ�����ϵʽ Ϊ��1��y=100��8��x��9����y=![]() ��9��x��45����
��9��x��45����
��2������ˮ�����ݲ���Ҫ�ȴ�3.25���ӣ�
��������
��1����D���������뷴����������һ����ʽ���ô���ϵ����ȷ�������������Ľ���ʽ��Ȼ����õ�C�͵�B�����꣬�Ӷ��ô���ϵ����ȷ��һ�κ����Ľ���ʽ��
��2����y=80���뷴���������Ľ���ʽ���Ӷ���ô𰸣�
��1��ֹͣ����ʱ����y=![]() ��
��
������ã�50=![]()
��ã�k=900��
��y=![]() ��
��
��y=100ʱ����ã�x=9��
��C��������9��100����
��B��������8��100����
��������ˮʱ����y=ax+20��
������ã�100=8a+20��
��ã�a=10��
����������ˮ��������ϵʽΪy=10x+20��0��x��8����
��ֹͣ���ȣ���y��x�ĺ�����ϵʽ Ϊ��1��y=100��8��x��9����y=![]() ��9��x��45����
��9��x��45����
��2����y=80����y=![]() ����x=11.25��
����x=11.25��
��˴���ˮ�����ݲ���Ҫ�ȴ�3.25���ӣ�


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η���
��һԪ���η���![]() ������ʵ����
������ʵ����![]() .
.
(1)��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(2)�����̵���ʵ����![]() ����
����![]() ,��
,��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��a+b��ab�����a��b����������������磺3+1.5��3��1.5�����3��1.5��һ�����������
��1����1���� ����һ�������������
��2����m��n��һ�������������2mn��![]() [3m+2��
[3m+2��![]() n��m��+3mn��6]��ֵ��
n��m��+3mn��6]��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ÿ��С�����α߳�Ϊ1�������У���A��B��C���ڸ���ϣ�
����AC�ij��ȵ���_____��
��������ͼ����һ��P��������AP��PB��PC������APƽ�֡�A����PC=PB��������ͼ��ʾ�������У����̶ȵ�ֱ�ߣ�������P������Ҫ˵����P��λ��������ҵ��ģ���Ҫ��֤����_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OΪԲ�Ķ��㣬MΪԲ������һ�㣬��P��OM�ϣ�һֻ��ţ��P���������Բ�������У��ص�P��ʱ�����������·�ߵĺۼ���ͼ��ʾ������OM��Բ���������չ�������ò���չ��ͼ�ǣ� ��

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
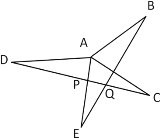
����Ŀ����ͼ����֪AB��AC��AD��AE��AB=AC��AD=AE��
��֤����1��BE=DC
��2��BE��DC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ����ش�����
�ӱ����̺�����Ȥ����ѧ���㣬���ø���Ҳ����������������������10���ӣ�4Сʱ�Ժ��Ǽ����ӣ���Ȼ![]() �����ڱ����Ͽ�������2����.����÷�����������ʾ�ӱ��ϵļӷ�����
�����ڱ����Ͽ�������2����.����÷�����������ʾ�ӱ��ϵļӷ�����![]() .����2����֮ǰ4Сʱ�Ǽ����ӣ��͵õ��ӱ��ϵļ���������÷���������ʾ�ӱ��ϵļ���.��ע��������0���Ӵ���12���ӣ����������Ͽ�֪��
.����2����֮ǰ4Сʱ�Ǽ����ӣ��͵õ��ӱ��ϵļ���������÷���������ʾ�ӱ��ϵļ���.��ע��������0���Ӵ���12���ӣ����������Ͽ�֪��
��1��![]() ______��
______��![]() ______��
______��
��2���������������У���ӵ������������Ϊ�෴����������ӱ�������������������5���෴����______������˵����������������ȥһ�������ڼ�����������෴�������ӱ��������Ƿ���Ȼ������
��3���涨���ӱ�������Ҳ��![]() �������ӱ��ϵ���������
�������ӱ��ϵ���������![]() ��
��![]() ��
��![]() ����
����![]() ���ж�
���ж�![]() �Ƿ�һ����������һ��������˵�����ɣ�����һ��������д��һ�鷴��������Ϸ�������˵��.
�Ƿ�һ����������һ��������˵�����ɣ�����һ��������д��һ�鷴��������Ϸ�������˵��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
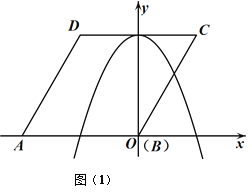
����Ŀ����ͼ(1)����֪����![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �Ḻ�����ϣ���
�Ḻ�����ϣ���![]() ������ԭ������
������ԭ������![]() ������Ϊ��
��������![]() ��
��![]() ����������
����������![]() ������
������![]() ���ϣ�������
���ϣ�������![]() �ߵ��е㣮
�ߵ��е㣮
��1�������������ߵĺ�������ʽ��
��2����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ���
�ĶԳƵ���![]() �����
�����![]() ����
����![]() ����̾��룻
����̾��룻
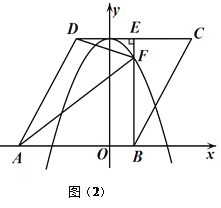
��3����ͼ��2��������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ���![]() ������������ƽ�ƣ�����
������������ƽ�ƣ�����![]() ��
��![]() �ڵ�
�ڵ�![]() �����������ڵ�
�����������ڵ�![]() ������
������![]() ��
��![]() ��������
��������![]() ƽ�Ƶ�ʱ��Ϊ
ƽ�Ƶ�ʱ��Ϊ![]() �루
�루![]() �������Ƿ����������
�������Ƿ����������![]() ��ʹ
��ʹ![]() ��
��![]() ���ƣ������ڣ����
���ƣ������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=kx2+��k��2��x��2������k��0����
��1�������������x��Ľ��㼰��������꣨�����ú�k�Ĵ���ʽ��ʾ����
��2�����Ǹ������߶��������ΪP��m��n����ֱ��д��|n|����Сֵ��
��3������������������ƽ��![]() ����λ���ȣ�������ƽ��
����λ���ȣ�������ƽ��![]() ����λ���ȣ�����k�ı仯��ƽ�ƺ�������ߵĶ��㶼��ij���º�����ͼ���ϣ����º����Ľ���ʽ����Ҫ��д�Ա�����ȡֵ��Χ����
����λ���ȣ�����k�ı仯��ƽ�ƺ�������ߵĶ��㶼��ij���º�����ͼ���ϣ����º����Ľ���ʽ����Ҫ��д�Ա�����ȡֵ��Χ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com