
【题目】已知抛物线y=kx2+(k﹣2)x﹣2(其中k>0).
(1)求该抛物线与x轴的交点及顶点的坐标(可以用含k的代数式表示);
(2)若记该抛物线顶点的坐标为P(m,n),直接写出|n|的最小值;
(3)将该抛物线先向右平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
个单位长度,随着k的变化,平移后的抛物线的顶点都在某个新函数的图象上,求新函数的解析式(不要求写自变量的取值范围).
【答案】(1)抛物线的顶点坐标是(![]() ,﹣
,﹣![]() );(2)当k=2时,|n|的最小值是2;(3)新函数的解析式为y=﹣
);(2)当k=2时,|n|的最小值是2;(3)新函数的解析式为y=﹣![]() ﹣1.
﹣1.
【解析】试题分析:(1)令y=0,解方程kx2+(k﹣2)x﹣2=0即可得到抛物线与x轴的交点,根据抛物线的顶点坐标公式(﹣![]() )代入进行计算即可求解;
)代入进行计算即可求解;
(2)根据(1)的结果,然后利用绝对值的性质,再根据不等式的性质进行解答;
(3)根据左加右减,上加下减,写出平移后的抛物线顶点坐标,然后消掉字母k即可得解.
试题解析:解:(1)当y=0时,kx2+(k﹣2)x﹣2=0,即(kx﹣2)(x+1)=0,解得:x1=![]() ,x2=﹣1,∴抛物线与x轴的交点坐标是(
,x2=﹣1,∴抛物线与x轴的交点坐标是(![]() ,0)与(﹣1,0),﹣
,0)与(﹣1,0),﹣![]() =﹣
=﹣![]() =
=![]() ﹣
﹣![]() =
=![]() =﹣
=﹣![]() ,∴抛物线的顶点坐标是(
,∴抛物线的顶点坐标是(![]() ﹣
﹣![]() ,﹣
,﹣![]() );
);
(2)根据(1),|n|=|﹣![]() |=
|=![]() =
=![]() =
=![]() +
+![]() +1≥2
+1≥2![]() +1=1+1=2,当且仅当
+1=1+1=2,当且仅当![]() =
=![]() ,即k=2时取等号,∴当k=2时,|n|的最小值是2;
,即k=2时取等号,∴当k=2时,|n|的最小值是2;
(3)![]() ﹣
﹣![]() +
+![]() =
=![]() ,﹣
,﹣![]() +
+![]() =
=![]() =
=![]() =﹣
=﹣![]() k﹣1,设平移后的抛物线的顶点坐标为(x,y),则
k﹣1,设平移后的抛物线的顶点坐标为(x,y),则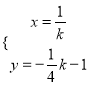 ,消掉字母k得:y=﹣
,消掉字母k得:y=﹣![]() ﹣1,∴新函数的解析式为y=﹣
﹣1,∴新函数的解析式为y=﹣![]() ﹣1.
﹣1.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
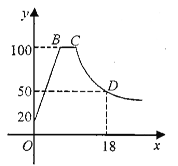
【题目】喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度 y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:课本上有这样一道例题:“解方程:![]()
解:去分母得:
6(x+15)=15-10(x-7)①
6x+90=15-10x+70②
16x=-5③
x=-![]() ④
④
请回答下列问题:
(1)得到①式的依据是________;
(2)得到②式的依据是________;
(3)得到③式的依据是________;
(4)得到④式的依据是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设![]() =k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
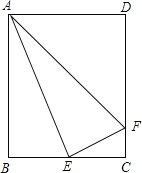
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所研制了一种抗生素新药,据临床观察:如果成人按规定的剂量注射这种抗生素,那么注射药液后每毫升血液中的含药量![]() 与时间
与时间![]() 之间的关系近似地满足如图所示的折线.
之间的关系近似地满足如图所示的折线.
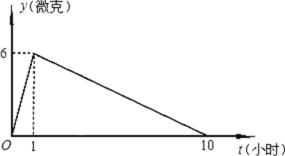
(1)写出注射药液后,每毫升血液中含药量![]() 与时间
与时间![]() 之间的函数解析式及自变量的取值范围;
之间的函数解析式及自变量的取值范围;
(2)据临床观察:每毫升血液中含药量不少于![]() 时,对控制病情是有效的,如果病人按规定的剂量注射该药液后,那么这一次注射的药液经过多长时间后控制病情开始有效?这个有效时间是多长?
时,对控制病情是有效的,如果病人按规定的剂量注射该药液后,那么这一次注射的药液经过多长时间后控制病情开始有效?这个有效时间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以直线![]() 上点
上点![]() 为端点作射线
为端点作射线![]() ,使
,使![]() ,将直角
,将直角![]() 的直角顶点放在点
的直角顶点放在点![]() 处.
处.
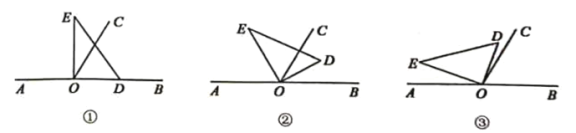
(1)若直角![]() 的边
的边![]() 在射线
在射线![]() 上(图①),求
上(图①),求![]() 的度数;
的度数;
(2)将直角![]() 绕点
绕点![]() 按逆时针方向转动,使得
按逆时针方向转动,使得![]() 所在射线平分
所在射线平分![]() (图②),说明
(图②),说明![]() 所在射线是
所在射线是![]() 的平分线;
的平分线;
(3)将直角![]() 绕点
绕点![]() 按逆时针方向转动到某个位置时,恰好使得
按逆时针方向转动到某个位置时,恰好使得![]() (图③),求
(图③),求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,丹东新一百商城销售![]() 两种商品,
两种商品,![]() 种商品每件进价
种商品每件进价![]() 元,售价
元,售价![]() 元;
元;![]() 种商品每件售价
种商品每件售价![]() 元,利润率为
元,利润率为![]() .
.
(1)每件![]() 种商品利润率为 ,
种商品利润率为 ,![]() 种商品每件进价为 元;
种商品每件进价为 元;
(2)由于热销,商城决定再购进上面的两种商品共![]() 件(每件商品的进价不变),采购部预算共支出
件(每件商品的进价不变),采购部预算共支出![]() 元,财务部算了一下,说:“如果你用这些钱买两种商品,那么账肯定算错了!”请你用学过的方程知识解释财务部为什么会这样说?
元,财务部算了一下,说:“如果你用这些钱买两种商品,那么账肯定算错了!”请你用学过的方程知识解释财务部为什么会这样说?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
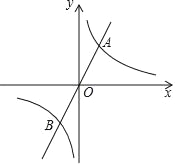
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com