
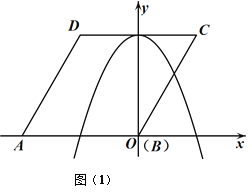
【题目】如图(1),已知菱形![]() 的边长为
的边长为![]() ,点
,点![]() 在
在![]() 轴负半轴上,点
轴负半轴上,点![]() 在坐标原点,点
在坐标原点,点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),抛物线
),抛物线![]() 顶点在
顶点在![]() 边上,并经过
边上,并经过![]() 边的中点.
边的中点.
(1)求这条抛物线的函数解析式;
(2)点![]() 关于直线
关于直线![]() 的对称点是
的对称点是![]() ,求点
,求点![]() 到点
到点![]() 的最短距离;
的最短距离;
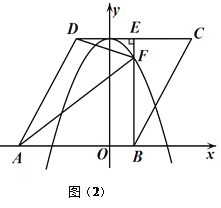
(3)如图(2)将菱形![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴正方向匀速平移,过点
轴正方向匀速平移,过点![]() 作
作![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() 、
、![]() .设菱形
.设菱形![]() 平移的时间为
平移的时间为![]() 秒(
秒(![]() ),问是否存在这样的
),问是否存在这样的![]() ,使
,使![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在t=1,使△ADF与△DEF相似
(3)存在t=1,使△ADF与△DEF相似
【解析】分析:(1)分别求出AB中点的坐标,抛物线的顶点坐标,再用待定系数法求抛物线的解析式;(2);判断点C′在以M为圆心,![]() 长为半径的圆上;(3)∠DEF=90°,∠DAF<90°,所以分两种情况讨论,利用相似三角形的对应比成比例列方程求解.
长为半径的圆上;(3)∠DEF=90°,∠DAF<90°,所以分两种情况讨论,利用相似三角形的对应比成比例列方程求解.
详解:(1)由题意得AB的中点坐标为(![]() ,0),抛物线的顶点坐标为(0,3),分别代入y=ax2+b,得
,0),抛物线的顶点坐标为(0,3),分别代入y=ax2+b,得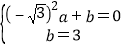 ,解得
,解得![]() .
.

∴这条抛物线的函数解析式为![]() .
.
(2)∵点C(![]() ,3)关于直线
,3)关于直线![]() 的对称点是C′,
的对称点是C′,![]() 过点(0,3),
过点(0,3),
∴C′一定在点(0,3)为圆心,![]() 为半径的圆上,
为半径的圆上,
由勾股定理得AM=![]() ,
,
当点A,C′,M在一条直线上时,AC′最小,最小值为AM-MC′,
即AC′的最小值为AM-MC′=![]() .
.
∴点C′到点A的最短距离为![]() .
.
(3)如图2所示,在Rt△BCE中,∠BEC=90°,BE=3,BC=![]() ,
,
∴![]() ,
,
∴∠C=60°,∠CBE=30°。∴EC=![]() BC=
BC=![]() ,DE=
,DE=![]() .
.
又∵AD∥BC,∴∠ADC+∠C=180°得∠ADC=180°-60°=120°,
要使△ADF与△DEF相似,则△ADF中必有一个角为直角,而∠DAF<60°,
∴∠ADF=90°或∠AFD=90°.
(I)若∠ADF=90°,∠EDF=120°-90°=30°,
在Rt△DEF中,DE=![]() ,得EF=1,DF=2,
,得EF=1,DF=2,
又∵E(t,3),F(t,-t2+3),
∴EF=3-(-t2+3)=t2,得∴t2=1,∵t>0,∴t=1,
此时![]() ,∴
,∴![]() .
.
又∵∠ADF=∠DEF,∴△ADF∽△DEF,
(II)若∠DFA=90°,可证得△DEF∽△FBA,则![]() ,
,
设EF=m,则FB=3-m,
∴![]() ,即m2-3m+6=0,此方程无实数根,
,即m2-3m+6=0,此方程无实数根,
∴此时t不存在.
综上所述,存在t=1,使△ADF与△DEF相似.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
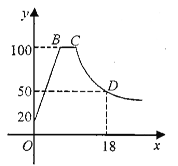
【题目】喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度 y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
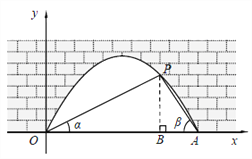
【题目】如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
,以O为原点,OA所在直线为x轴建立直角坐标系.若水面上升1m,水面宽为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
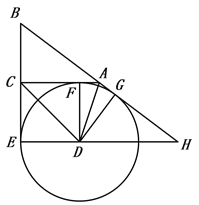
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,⊙
,⊙![]() 与
与![]() 、
、![]() 、
、![]() 都相切,切点分别是
都相切,切点分别是![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两个根.
的两个根.
(1)求证:![]() 是直角三角形;
是直角三角形;
(2)若![]() ,求四边形CEDF的面积.
,求四边形CEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点燃蜡烛,按照与时间成正比例关系变短,长21cm的蜡烛,已知点燃6分钟后,蜡烛变短3.6cm,设蜡烛点燃x分钟后变短ycm,求:
(1)用x表示函数y的解析式;
(2)自变量的取值范围;
(3)此蜡烛几分钟燃烧完?
(4)画出此函数的图像。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读题:课本上有这样一道例题:“解方程:![]()
解:去分母得:
6(x+15)=15-10(x-7)①
6x+90=15-10x+70②
16x=-5③
x=-![]() ④
④
请回答下列问题:
(1)得到①式的依据是________;
(2)得到②式的依据是________;
(3)得到③式的依据是________;
(4)得到④式的依据是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
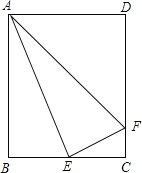
【题目】如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设![]() =k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
A.(1)(2)(3) B.(1)(3) C.(1)(2) D.(2)(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
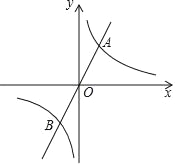
【题目】如图,已知正比例函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com