
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒1cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t(t>0)秒.
(1)AC= cm;
(2)若点P恰好在AB的垂直平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP是以AC为腰的等腰三角形(直接写出结果)?

【答案】(1)3;(2)t为![]() 秒或
秒或![]() 秒;(3)t为3秒或
秒;(3)t为3秒或![]() 秒或6秒.
秒或6秒.
【解析】
(1)根据勾股定理可以得到![]() ,代入数值计算即可;
,代入数值计算即可;
(2)点P恰好在AB的垂直平分线上时,分两种情况讨论:①当点P运动到点D时;②当点P运动到点E时,根据图形计算即可;
(3)若△ACP是等腰三角形,分情况讨论:①当AP=AC时;②当CA=CP时,利用勾股定理,三角形面积相等来计算即可.
(1)如甲图所示:
∵∠ACB=90°,
∴△ABC是直角三角形,
在![]() ABC中,由勾股定理得,
ABC中,由勾股定理得,
![]() ,
,
又AB=5cm,BC=4cm,
![]() ,
,
故答案为3;


(2)点P恰好在AB的垂直平分线上时,
如乙图所示:
∵DE是线段AB的垂直平分线,
∴AD=BD=![]() ,AE=BE,
,AE=BE,
①当点P运动到点D时,
∵AB=5cm,点P从点A出发,以每秒1cm的速度运动,
∴![]() =
=![]() 秒,
秒,
②当点P运动到点E时,设BE=x,则EC=4﹣x,
∵AE=BE,
∴AE=x,
在Rt△AEC中,由勾股定理得,![]()
∵AC=3,AE=x,EC=4﹣x,
∴32+(4﹣x)2=![]() , 解得:x=
, 解得:x=![]() ,
,
∴AB+BE=![]() ,
,
∴![]() 秒,
秒,

即点P在AB的垂直平分线上时,运动时间t为![]() 秒或
秒或![]() 秒,
秒,
故答案为:![]() 秒或
秒或![]() 秒;
秒;
(3)运动过程中,△ACP是等腰三角形,
①当AP=AC时,如丙图(1)所示:
∵AC=3,
∴AP=3,
∴![]() =3秒,
=3秒,

②当CA=CP时,如丙图(2)所示:
若点P运动到![]() 时,AC=
时,AC=![]() C,过点C作CH⊥AB
C,过点C作CH⊥AB
交AB于点H,
∵![]() ,
,
AB=5cm,BC=4cm,AC=3cm,
∴CH=![]() cm,
cm,
在Rt△AHC中,由勾股定理得,
AH=![]() cm,
cm,
又∵A![]() =2AH=
=2AH=![]() cm,
cm,
∴![]() 秒,
秒,
若点P运动到![]() 时,AC=
时,AC=![]() C,
C,
∵AC=3cm,
∴![]() C=3cm,
C=3cm,
又∵B![]() =BC﹣
=BC﹣![]() C,
C,
∴B![]() =1cm,
=1cm,
∴AP+B![]() =5+1=6cm,
=5+1=6cm,
∴![]() =6秒,
=6秒,
综合所述,△ACP是以AC为腰的等腰三角形时,t为3秒或![]() 秒或6秒,
秒或6秒,
故答案为:3秒或![]() 秒或6秒.
秒或6秒.


科目:初中数学 来源: 题型:
【题目】甲乙两家商场中品牌质量规格等都相同的商品,在甲乙两商场的标价都相同,在双12时两家商场进行促销活动.甲商场采用“买200减100”的促销方式,即购买商品的总金额满200元,但不足400元,少付100元,满400元,但不足600元,少付200元;乙商场按顾客购买商品的总金额打6折促销,
(1)若顾客在甲商场购买了510元的商品,付款时应付多少钱?
(2)(列方程解应用题)小明与小亮分别在甲,乙两家商场中各买了一双鞋,根据下面两人的对话求出鞋的标价.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.(1)甲蚂蚁选择“向左”爬行的概率为________;
(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分![]() 分)小明、小华在一栋高楼前感慨楼房真高.小明说:“这楼起码
分)小明、小华在一栋高楼前感慨楼房真高.小明说:“这楼起码![]() 层!”小华却不以为然:“
层!”小华却不以为然:“![]() 层?我看没有!”小明说:“有本事,就让我们一起来测量吧!”
层?我看没有!”小明说:“有本事,就让我们一起来测量吧!”
如图,矩形![]() 表示楼体,小明、小华在楼体两侧各选
表示楼体,小明、小华在楼体两侧各选![]() 、
、![]() 两点,使得
两点,使得![]() 、
、![]() 、
、![]() 、
、![]() 四点在同一直线上,利用皮尺和侧倾器测得如下数据,
四点在同一直线上,利用皮尺和侧倾器测得如下数据, ![]() 米,
米, ![]() 米,
米, ![]() ,
, ![]() .
.
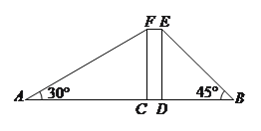
(![]() )请你帮助他们算一算楼高.(结果保留根号)
)请你帮助他们算一算楼高.(结果保留根号)
(![]() )若每层楼按
)若每层楼按![]() 米计算,你支持小明还是小华的观点呢?请说明理由.
米计算,你支持小明还是小华的观点呢?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:(1)如图,已知:在等腰直角![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .小明观察图形特征后猜想线段
.小明观察图形特征后猜想线段![]() 、
、![]() 和
和![]() 之间存在
之间存在![]() 的数量关系,请你判断他的猜想是否正确,并说明理由.
的数量关系,请你判断他的猜想是否正确,并说明理由.

(2)如图,将(1)中的条件改为:![]() 为等边三角形,
为等边三角形,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,并且有
上,并且有![]() ,请问结论
,请问结论![]() 是否成立?并说明理由.
是否成立?并说明理由.

(3)如图,若将(1)中的三角形变形为一般的等腰三角形,![]() 中,
中,![]() ,
,![]() ,其中
,其中![]() 为任意锐角或钝角,
为任意锐角或钝角,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上.问:满足什么条件时,结论
上.问:满足什么条件时,结论![]() 仍成立?直接写出条件即可.
仍成立?直接写出条件即可.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 平分
平分![]() .将一块足够大的三角尺的直角顶点落在射线
.将一块足够大的三角尺的直角顶点落在射线![]() 的任意一点
的任意一点![]() 上,并使三角尺的一条直角边与
上,并使三角尺的一条直角边与![]() (或
(或![]() 的延长线)交于点
的延长线)交于点![]() ,另一条直角边与
,另一条直角边与![]() 交于点
交于点![]() .
.

(1)如图1,当![]() 与边
与边![]() 垂直时,证明:
垂直时,证明:![]() ;
;
(2)如图2,把三角尺绕点![]() 旋转,三角尺的两条直角边分别交
旋转,三角尺的两条直角边分别交![]() 于点
于点![]() ,在旋转过程中,
,在旋转过程中,![]() 与
与![]() 相等吗?请直接写出结论:
相等吗?请直接写出结论:![]()
![]() (填
(填![]() ,
,![]() ,
,![]() ),
),
(3)如图3,三角尺绕点![]() 继续旋转,三角尺的一条直角边与
继续旋转,三角尺的一条直角边与![]() 的延长线交于点
的延长线交于点![]() ,另一条直角边与
,另一条直角边与![]() 交于点
交于点![]() .在旋转过程中,
.在旋转过程中,![]() 与
与![]() 相等吗?若相等,请给出证明;若不相等,请说明理由.
相等吗?若相等,请给出证明;若不相等,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的平分线与BC的中垂线DE交于点E,过点E作AC边的垂线,垂足为N,过点E作AB延长线的垂线,垂足为M.
(1)求证:BM=CN;
(2)若,AB=2,AC=8,求BM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
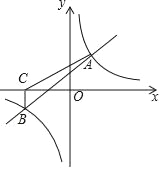
【题目】如图,一次函数y=x+2与反比例函数y=![]() 的图象相交于A(2,m),B(﹣4,n)两点.
的图象相交于A(2,m),B(﹣4,n)两点.
(1)求反比例函数的解析式;
(2)根据所给条件,请直接写出不等式x+2>![]() 的解集: ;
的解集: ;
(3)过点B作BC⊥x轴,垂足为C,连接AC,求S△ABC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com