
【题目】综合与实践:
概念理解:将△ABC 绕点 A 按逆时针方向旋转,旋转角记为 θ(0°≤θ≤90°),并使各边长变为原来的 n 倍,得到△AB′C′,如图,我们将这种变换记为[θ,n],![]() :
:![]() .
.

问题解决:(2)如图,在△ABC 中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得到△AB′C′,使点 B,C,C′在同一直线上,且四边形 ABB′C′为矩形,求 θ 和 n 的值.

拓广探索:(3)在△ABC 中,∠BAC=45°,∠ACB=90°,对△ABC作变换 得到△AB′C′,则四边形 ABB′C′为正方形
科目:初中数学 来源: 题型:
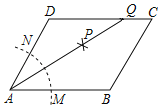
【题目】如图,在平行四边形ABCD中,按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;
②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;
MN的长为半径作弧,两弧相交于点P;
③作AP射线,交边CD于点Q.
若QC=1,BC=3,则平行四边形ABCD周长为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦AC为6cm,
(1)用尺规作图画出∠ACB的平分线交⊙O于点D.(不要写作法,保留作图痕迹)
(2)分别连接点AD和BD,求弦BC、AD、BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关公,作为运城乃至山西的一张名片,吸引了来自世界各地的游客,在运城西南![]() 公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高
公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高![]() 米,象征关公享年
米,象征关公享年![]() 岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图,
岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图,![]() 代表底座的高,坡顶
代表底座的高,坡顶![]() 与底座底部
与底座底部![]() 处在同一水平面上,该游客在斜坡底
处在同一水平面上,该游客在斜坡底![]() 处测得该底座顶端
处测得该底座顶端![]() 的仰角为
的仰角为![]() ,然后他沿着坡度为
,然后他沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该底座顶端
处又测得该底座顶端![]() 的仰角为
的仰角为![]() .求:
.求:
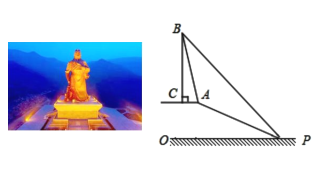
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 求底座
求底座![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(3)若AC=5,AB=6,求菱形ADCF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
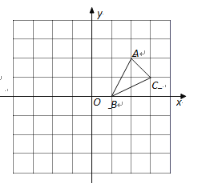
【题目】如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1)
(1)画出△ABC关于x轴对称的![]() ;
;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B1C2,写出点C2的坐标;
(3)在(1)(2)的基础上,图中的![]() ,
,![]() 关于哪个点中心对称.
关于哪个点中心对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.

(1)观察图形,写出图中所有与∠AED相等的角.
(2)选择图中与∠AED相等的任意一个角,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的引桥部分的示意图,梯面AD、BE相互平行,且与地面成37°的夹角,DE是一段水平歇台,离地面高度3米.已知天桥高度BC为4.8米,引桥水平跨度AC为8米,求梯面AD、BE及歇台DE的长.(参考数据:![]() ,结果保留两位小数)
,结果保留两位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
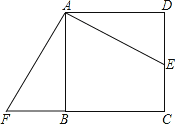
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com