
【题目】如图,⊙O的直径AB为10cm,弦AC为6cm,
(1)用尺规作图画出∠ACB的平分线交⊙O于点D.(不要写作法,保留作图痕迹)
(2)分别连接点AD和BD,求弦BC、AD、BD的长.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=![]() ,OB=4,OE=1.
,OB=4,OE=1.
(1)求一次函数的解析式和反比例函数的解析式
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
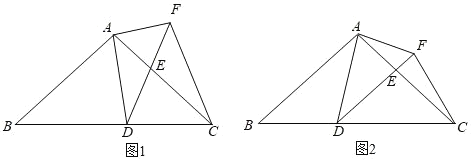
【题目】如图1,在△ABC中,AB=AC=10,BC=16,点D为BC边上的动点(点D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
概念理解:将△ABC 绕点 A 按逆时针方向旋转,旋转角记为 θ(0°≤θ≤90°),并使各边长变为原来的 n 倍,得到△AB′C′,如图,我们将这种变换记为[θ,n],![]() :
:![]() .
.

问题解决:(2)如图,在△ABC 中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得到△AB′C′,使点 B,C,C′在同一直线上,且四边形 ABB′C′为矩形,求 θ 和 n 的值.

拓广探索:(3)在△ABC 中,∠BAC=45°,∠ACB=90°,对△ABC作变换 得到△AB′C′,则四边形 ABB′C′为正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识回顾)
七年级学习代数式求值时,遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值”,通常的解题方法是把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含x项的系数为0,即原式=(a+3)x﹣6y+5,所以a+3=0,则a=﹣3.
(理解应用)
(1)若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,试求m的值;
(2)若一次函数y=2kx+1﹣4k的图象经过某个定点,则该定点坐标为 ;
(能力提升)
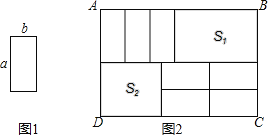
(3)7张如图1的小长方形,长为a,宽为b.按照图2方式不重叠地放在大矩形ABCD内,大矩形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变.求a与b的等量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com