
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针旋转60°到△
,将△ABC绕点A顺时针旋转60°到△![]() 的位置,连接
的位置,连接![]() ,则
,则![]() 的长为( )
的长为( )
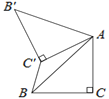
A.2B.![]() C.
C.![]() D.1
D.1
科目:初中数学 来源: 题型:
【题目】已知A1,A2,A3是抛物线y=![]() x2+1(x>0)上的三点,且A1,A2,A3三点的横坐标为连续的整数,连接A1A3,过A2作A2Q⊥x轴于点Q,交A1A3于点P,则线段PA2的长为__.
x2+1(x>0)上的三点,且A1,A2,A3三点的横坐标为连续的整数,连接A1A3,过A2作A2Q⊥x轴于点Q,交A1A3于点P,则线段PA2的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
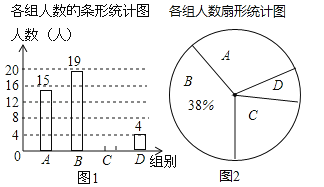
【题目】小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示A组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
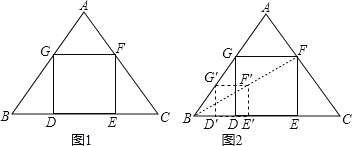
【题目】如图,△ABC是一块等边三角形的废铁片,其中AB=AC=10![]() ,BC=12
,BC=12![]() .利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F. G分别落在AC、AB上.
.利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F. G分别落在AC、AB上.
(1)小聪想:要画出正方形DEFG,只要能计算出正方形的边长就能求出BD和CE的长,从而确定D点和E点,再画正方形DEFG就容易了.请你帮小聪求出正方形的边长.
(2)小明想:不求正方形的边长也能画出正方形.具体作法是:
①在AB边上任取一点G′,如图2作正方形G′D′E′F′;
②连接BF′并延长交AC于点F;
③过点F作FE∥F′E′交BC于点E,FG∥F′G′交AB于点G,GD∥G′D′交BC于点D,则四边形DEFG即为所求的正方形.你认为小明的作法正确吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦AC为6cm,
(1)用尺规作图画出∠ACB的平分线交⊙O于点D.(不要写作法,保留作图痕迹)
(2)分别连接点AD和BD,求弦BC、AD、BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
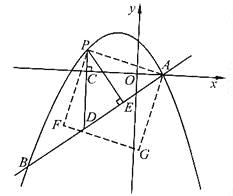
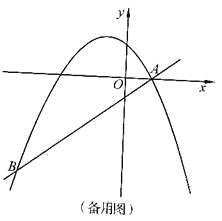
【题目】如图,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关公,作为运城乃至山西的一张名片,吸引了来自世界各地的游客,在运城西南![]() 公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高
公里的常平村(关公故乡)南山上,有一尊巨型关公铜像,高![]() 米,象征关公享年
米,象征关公享年![]() 岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图,
岁,底座的高度也有一定寓意.有一位游客,对此产生了兴趣,想测量它的高度,由于游客无法直接到达铜像底部,因此该游客计划借助坡面高度来测量它的高度.如图,![]() 代表底座的高,坡顶
代表底座的高,坡顶![]() 与底座底部
与底座底部![]() 处在同一水平面上,该游客在斜坡底
处在同一水平面上,该游客在斜坡底![]() 处测得该底座顶端
处测得该底座顶端![]() 的仰角为
的仰角为![]() ,然后他沿着坡度为
,然后他沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该底座顶端
处又测得该底座顶端![]() 的仰角为
的仰角为![]() .求:
.求:
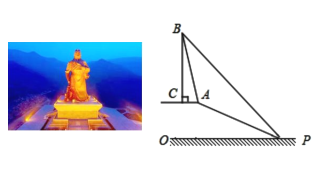
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 求底座
求底座![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
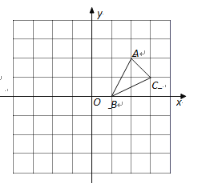
【题目】如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1)
(1)画出△ABC关于x轴对称的![]() ;
;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B1C2,写出点C2的坐标;
(3)在(1)(2)的基础上,图中的![]() ,
,![]() 关于哪个点中心对称.
关于哪个点中心对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE
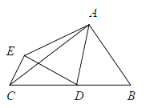
(1)求证:AD=ED
(2)连接BE,猜想△BEC的形状,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com