
ЁОЬтФПЁПЙиЙЋЃЌзїЮЊдЫГЧФЫжСЩНЮїЕФвЛеХУћЦЌЃЌЮќв§СЫРДздЪРНчИїЕиЕФгЮПЭЃЌдкдЫГЧЮїФЯ![]() ЙЋРяЕФГЃЦНДх(ЙиЙЋЙЪЯч)ФЯЩНЩЯЃЌгавЛз№ОоаЭЙиЙЋЭЯёЃЌИп
ЙЋРяЕФГЃЦНДх(ЙиЙЋЙЪЯч)ФЯЩНЩЯЃЌгавЛз№ОоаЭЙиЙЋЭЯёЃЌИп![]() УзЃЌЯѓеїЙиЙЋЯэФъ
УзЃЌЯѓеїЙиЙЋЯэФъ![]() ЫъЃЌЕззљЕФИпЖШвВгавЛЖЈдЂвтЃЎгавЛЮЛгЮПЭЃЌЖдДЫВњЩњСЫаЫШЄЃЌЯыВтСПЫќЕФИпЖШЃЌгЩгкгЮПЭЮоЗЈжБНгЕНДяЭЯёЕзВПЃЌвђДЫИУгЮПЭМЦЛЎНшжњЦТУцИпЖШРДВтСПЫќЕФИпЖШ.ШчЭМЃЌ
ЫъЃЌЕззљЕФИпЖШвВгавЛЖЈдЂвтЃЎгавЛЮЛгЮПЭЃЌЖдДЫВњЩњСЫаЫШЄЃЌЯыВтСПЫќЕФИпЖШЃЌгЩгкгЮПЭЮоЗЈжБНгЕНДяЭЯёЕзВПЃЌвђДЫИУгЮПЭМЦЛЎНшжњЦТУцИпЖШРДВтСПЫќЕФИпЖШ.ШчЭМЃЌ![]() ДњБэЕззљЕФИпЃЌЦТЖЅ
ДњБэЕззљЕФИпЃЌЦТЖЅ![]() гыЕззљЕзВП
гыЕззљЕзВП![]() ДІдкЭЌвЛЫЎЦНУцЩЯЃЌИУгЮПЭдкаБЦТЕз
ДІдкЭЌвЛЫЎЦНУцЩЯЃЌИУгЮПЭдкаБЦТЕз![]() ДІВтЕУИУЕззљЖЅЖЫ
ДІВтЕУИУЕззљЖЅЖЫ![]() ЕФбіНЧЮЊ
ЕФбіНЧЮЊ![]() ЃЌШЛКѓЫћбизХЦТЖШЮЊ
ЃЌШЛКѓЫћбизХЦТЖШЮЊ![]() ЕФаБЦТ
ЕФаБЦТ![]() ХЪааСЫ
ХЪааСЫ![]() УзЃЌдкЦТЖЅ
УзЃЌдкЦТЖЅ![]() ДІгжВтЕУИУЕззљЖЅЖЫ
ДІгжВтЕУИУЕззљЖЅЖЫ![]() ЕФбіНЧЮЊ
ЕФбіНЧЮЊ![]() ЃЎЧѓЃК
ЃЎЧѓЃК
![]() ЦТЖЅ
ЦТЖЅ![]() ЕНЕиУц
ЕНЕиУц![]() ЕФОрРыЃЛ
ЕФОрРыЃЛ
![]() ЧѓЕззљ
ЧѓЕззљ![]() ЕФИпЖШ(НсЙћОЋШЗЕН
ЕФИпЖШ(НсЙћОЋШЗЕН![]() Уз)ЃЎ
Уз)ЃЎ
(ВЮПМЪ§Он:![]() ЃЌ
ЃЌ![]()
ЁОД№АИЁПЃЈ1ЃЉЦТЖЅ![]() ЕНЕиУц
ЕНЕиУц![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() УзЃЛЃЈ2ЃЉЕззљ
УзЃЛЃЈ2ЃЉЕззљ![]() ЕФИпЖШдМЮЊ
ЕФИпЖШдМЮЊ![]() УзЃЎ
УзЃЎ
ЁОНтЮіЁП
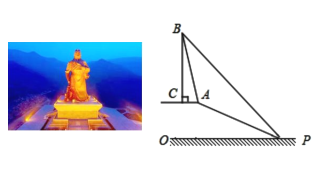
ЃЈ1ЃЉШчЭМЫљЪОзїГіИЈжњЯпЃЌИљОнаБЦТAPЕФЦТЖШЃЌЩшГіЮДжЊЪ§ЃЌгЩЙДЙЩЖЈРэЧѓГіAPЃЌдйСаГіЗНГЬНтД№МДПЩЃЛ
ЃЈ2ЃЉзїГіИЈжњЯпЃЌжЄУїЫФБпаЮ![]() ЪЧОиаЮЃЌЕУГіЁЯBPD=45ЁуЃЌЩш
ЪЧОиаЮЃЌЕУГіЁЯBPD=45ЁуЃЌЩш![]() ЃЌБэЪОГіACЃЌдйРћгУBCЁЂACБэЪОГіtan76ЁуЃЌСаГіЗНГЬЧѓНтМДПЩЃЎ
ЃЌБэЪОГіACЃЌдйРћгУBCЁЂACБэЪОГіtan76ЁуЃЌСаГіЗНГЬЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌ
ЃЌ
![]() аБЦТ
аБЦТ![]() ЕФЦТЖШЮЊ
ЕФЦТЖШЮЊ![]()
![]()
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌгЩЙДЙЩЖЈРэЃЌЕУ
ЃЌгЩЙДЙЩЖЈРэЃЌЕУ![]() ЃЌ
ЃЌ
![]() ЃЌНтЕУk=2
ЃЌНтЕУk=2
![]() ЃЌ
ЃЌ
Д№ЃКЦТЖЅ![]() ЕНЕиУц
ЕНЕиУц![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() УзЃЎ
УзЃЎ
ЃЈ2ЃЉбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЫФБпаЮ
ЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гЩЃЈ1ЃЉжЊ![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУ![]() УзЃЌ
УзЃЌ
Д№ЃКЕззљ![]() ЕФИпЖШдМЮЊ
ЕФИпЖШдМЮЊ![]() УзЃЎ
УзЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
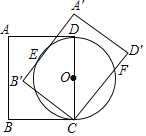
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН5ЃЌBCЃН4ЃЌвдCDЮЊжБОЖзїЁбOЃЎНЋОиаЮABCDШЦЕуCа§зЊЃЌЪЙЫљЕУОиаЮAЁфBЁфCDЁфЕФБпAЁфBЁфгыЁбOЯрЧаЃЌЧаЕуЮЊEЃЌБпCDЁфгыЁбOЯрНЛгкЕуFЃЌдђCFЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН3cmЃЌADЃН4cmЃЌEFОЙ§ЖдНЧЯпBDЕФжаЕуOЃЌЗжБ№НЛADЃЌBCгкЕуEЃЌFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїBOFЁеЁїDOEЃЛ
ЃЈ2ЃЉЕБEFЁЭBDЪБЃЌЧѓAEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
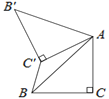
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCжаЃЌЁЯC=90ЁуЃЌAC=BC=![]() ЃЌНЋЁїABCШЦЕуAЫГЪБеыа§зЊ60ЁуЕНЁї
ЃЌНЋЁїABCШЦЕуAЫГЪБеыа§зЊ60ЁуЕНЁї![]() ЕФЮЛжУЃЌСЌНг
ЕФЮЛжУЃЌСЌНг![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ
A.2B.![]() C.
C.![]() D.1
D.1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋвЛИБШ§НЧГпЃЈдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдк
ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЉШчЭМАкЗХЃЌЕу
ЃЉШчЭМАкЗХЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыЗНЯђа§зЊ
ЫГЪБеыЗНЯђа§зЊ![]() ЃЈ
ЃЈ![]() ЃЉЃЌ
ЃЉЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊЃЈ ЃЉ
ЕФжЕЮЊЃЈ ЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
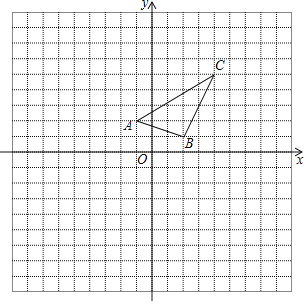
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ1ЕФе§ЗНаЮЭјИёжаНЈСЂЦНУцжБНЧзјБъЯЕЃЌвбжЊЁїABCШ§ИіЖЅЕуЗжБ№ЮЊAЃЈЉ1ЃЌ2ЃЉЁЂBЃЈ2ЃЌ1ЃЉЁЂCЃЈ4ЃЌ5ЃЉЃЎ
ЃЈ1ЃЉвддЕуOЮЊЮЛЫЦжааФЃЌдкxжсЕФЩЯЗНЛГіЁїA1B1C1ЃЌЪЙЁїA1B1C1гыЁїABCЮЛЫЦЃЌЧвЯрЫЦБШЮЊ2ЃЛ
ЃЈ2ЃЉЁїA1B1C1ЕФУцЛ§ЪЧЁЁ ЁЁЦНЗНЕЅЮЛЃЎ
ЃЈ3ЃЉЕуPЃЈaЃЌbЃЉЮЊЁїABCФквЛЕуЃЌдђдкЁїA1B1C1ФкЕФЖдгІЕуPЁЏЕФзјБъЮЊЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзлКЯгыЪЕМљЃК
ИХФюРэНтЃКНЋЁїABC ШЦЕу A АДФцЪБеыЗНЯђа§зЊЃЌа§зЊНЧМЧЮЊ ІШЃЈ0ЁуЁмІШЁм90ЁуЃЉЃЌВЂЪЙИїБпГЄБфЮЊдРДЕФ n БЖЃЌЕУЕНЁїABЁфCЁфЃЌШчЭМЃЌЮвУЧНЋетжжБфЛЛМЧЮЊЃлІШЃЌnЃнЃЌ![]() ЃК
ЃК![]() ЃЎ
ЃЎ

ЮЪЬтНтОіЃКЃЈ2ЃЉШчЭМЃЌдкЁїABC жаЃЌЁЯBAC=30ЁуЃЌЁЯACB=90ЁуЃЌЖдЁїABC зїБфЛЛЃлІШЃЌnЃнЕУЕНЁїABЁфCЁфЃЌЪЙЕу BЃЌCЃЌCЁфдкЭЌвЛжБЯпЩЯЃЌЧвЫФБпаЮ ABBЁфCЁфЮЊОиаЮЃЌЧѓ ІШ КЭ n ЕФжЕЃЎ

ЭиЙуЬНЫїЃКЃЈ3ЃЉдкЁїABC жаЃЌЁЯBAC=45ЁуЃЌЁЯACB=90ЁуЃЌЖдЁїABCзїБфЛЛ ЕУЕНЁїABЁфCЁфЃЌдђЫФБпаЮ ABBЁфCЁфЮЊе§ЗНаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯMONЃН90ЁуЃЌAЪЧЁЯMONФкВПЕФвЛЕуЃЌЙ§ЕуAзїABЁЭONЃЌДЙзуЮЊЕуBЃЌABЃН3РхУзЃЌOBЃН4РхУзЃЌЖЏЕуEЃЌFЭЌЪБДгOЕуГіЗЂЃЌЕуEвд1.5РхУз/УыЕФЫйЖШбиONЗНЯђдЫЖЏЃЌЕуFвд2РхУз/УыЕФЫйЖШбиOMЗНЯђдЫЖЏЃЌEFгыOAНЛгкЕуCЃЌСЌНгAEЃЌЕБЕуEЕНДяЕуBЪБЃЌЕуFЫцжЎЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊtУыЃЈtЃО0ЃЉЃЎ

ЃЈ1ЃЉЕБtЃН1УыЪБЃЌЁїEOFгыЁїABOЪЧЗёЯрЫЦЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉдкдЫЖЏЙ§ГЬжаЃЌВЛТлtШЁКЮжЕЪБЃЌзмгаEFЁЭOAЃЎЮЊЪВУДЃП
ЃЈ3ЃЉСЌНгAFЃЌдкдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЕУSЁїAEFЃН![]() SЫФБпаЮAEOFЃПШєДцдкЃЌЧыЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
SЫФБпаЮAEOFЃПШєДцдкЃЌЧыЧѓГіДЫЪБtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊ(Љ1ЃЌ![]() )ЃЌвддЕуOЮЊжааФЃЌНЋЕуAЫГЪБеыа§зЊ150ЁуЕУЕНЕуAЁфЃЌдђЕуAЁфЕФзјБъЮЊ( )
)ЃЌвддЕуOЮЊжааФЃЌНЋЕуAЫГЪБеыа§зЊ150ЁуЕУЕНЕуAЁфЃЌдђЕуAЁфЕФзјБъЮЊ( )

A.(0ЃЌЉ2)B.(1ЃЌЉ![]() )C.(2ЃЌ0)D.(
)C.(2ЃЌ0)D.(![]() ЃЌЉ1)
ЃЌЉ1)
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com