
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
先根据直角三角形斜边上的中线性质得CD=AD=DB,则∠ACD=∠A=30°,∠BCD=∠B=60°,由于∠EDF=90°,可利用互余得∠CPD=60°,再根据旋转的性质得∠PDM=∠CDN=α,于是可判断△PDM∽△CDN,得到![]() =
=![]() ,然后在Rt△PCD中利用正切的定义得到tan∠PCD=tan30°=
,然后在Rt△PCD中利用正切的定义得到tan∠PCD=tan30°=![]() ,于是可得
,于是可得![]() =
=![]() .
.
∵点D为斜边AB的中点,
∴CD=AD=DB,
∴∠ACD=∠A=30°,∠BCD=∠B=60°,
∵∠EDF=90°,
∴∠CPD=60°,
∴∠MPD=∠NCD,
∵△EDF绕点D顺时针方向旋转α(0°<α<60°),
∴∠PDM=∠CDN=α,
∴△PDM∽△CDN,
∴![]() =
=![]() ,
,
在Rt△PCD中,∵tan∠PCD=tan30°=![]() ,
,
∴![]() =tan30°=
=tan30°=![]() .
.
故选:C.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:
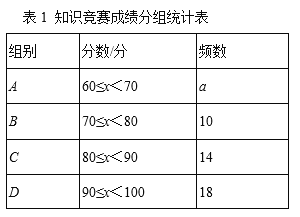

(1)本次调查一共随机抽取了_____个参赛学生的成绩;
(2)表1中a=_____;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是_____;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,动点
;同时,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停止运动.设点
;当一个点停止运动,另一个点也停止运动.设点![]() ,
,![]() 运动的时间是
运动的时间是![]()
![]()
![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
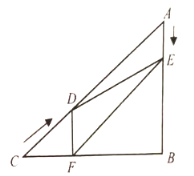
(1)![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.


(3)解决问题如图3,在正方形ABCD中,CD=![]() .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量![]() 与单价
与单价![]() 满足一次函数关系,求出
满足一次函数关系,求出![]() 与
与![]() 的关系式;
的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一张周长为18cm的三角形纸片,BC=5cm,⊙O是它的内切圆,小明用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线![]() 剪下△AMN,则剪下的三角形的周长为( )
剪下△AMN,则剪下的三角形的周长为( )
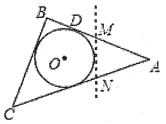
A.![]() B.
B.![]() C.
C.![]() D.随直线
D.随直线![]() 的变化而变化
的变化而变化
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,DN=3![]() ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=( )
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=( )
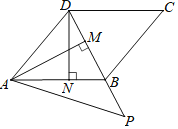
A.4.5B.5.5C.6D.6.5
查看答案和解析>>
科目:初中数学 来源: 题型:
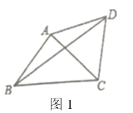
【题目】(1)(学习心得)于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.例如:如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 外一点,且
外一点,且![]() ,求
,求![]() 的度数.若以点
的度数.若以点![]() 为圆心,
为圆心,![]() 为半径作辅助
为半径作辅助![]() ,则
,则![]() 、
、![]() 必在
必在![]() 上,
上,![]() 是
是![]() 的圆心角,而
的圆心角,而![]() 是圆周角,从而可容易得到
是圆周角,从而可容易得到![]() =________
=________![]() .
.
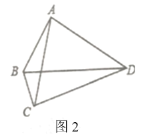
(2)(问题解决)如图2,在四边形![]() 中,
中,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
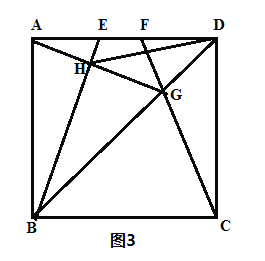
(3)(问题拓展)如图3,![]() 是正方形
是正方形![]() 的边
的边![]() 上两个动点,满足
上两个动点,满足![]() .连接交于点,连接
.连接交于点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交于点
交于点![]() ,若正方形的边长为2,则线段
,若正方形的边长为2,则线段![]() 长度的最小值是_______.
长度的最小值是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com