
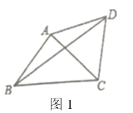
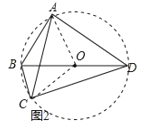
����Ŀ����1����ѧϰ�ĵã���ͮͬѧ��ѧϰ����Բ����һ�����ݺо���һЩ��������������Ӹ���Բ������Բ��֪ʶ���������ʹ�����÷dz�����.���磺��ͼ1����![]() �У�
�У�![]() ,
,![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ,��
,��![]() �Ķ���.���Ե�
�Ķ���.���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶������
Ϊ�뾶������![]() ����
����![]() ��
��![]() ����
����![]() �ϣ�
�ϣ�![]() ��
��![]() ��Բ�Ľǣ���
��Բ�Ľǣ���![]() ��Բ�ܽǣ��Ӷ������õ�
��Բ�ܽǣ��Ӷ������õ�![]() =________
=________![]() .
.
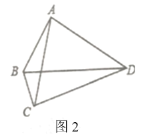
��2��������������ͼ2�����ı���![]() �У�
�У�![]() ,
,![]() ,��
,��![]() �Ķ���.
�Ķ���.
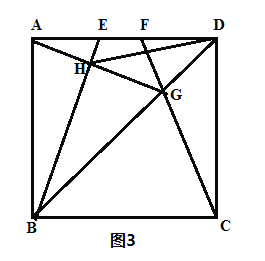
��3����������չ����ͼ3��![]() ��������
��������![]() �ı�
�ı�![]() ���������㣬����
���������㣬����![]() .���ӽ��ڵ㣬����
.���ӽ��ڵ㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ,����
,����![]() ���ڵ�
���ڵ�![]() ,�������εı߳�Ϊ2�����߶�
,�������εı߳�Ϊ2�����߶�![]() ���ȵ���Сֵ��_______.
���ȵ���Сֵ��_______.
���𰸡���1��45����2��25������3��![]()
��������
��1������ͬ�����Ե�Բ�ܽ�������Բ�Ľǵ�һ����⣮
��2����A��B��C��D��Բ���ó���BDC����BAC��
��3�����������ε����ʿɵ�AB��AD��CD����BAD����CDA����ADG����CDG��Ȼ�����á��߽DZߡ�֤����ABE�͡�DCFȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵá�1����2�����á�SAS��֤����ADG�͡�CDGȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵá�2����3���Ӷ��õ���1����3��Ȼ�������AHB��90�㣬ȡAB���е�O������OH��OD������ֱ��������б���ϵ����ߵ���б�ߵ�һ��ɵ�OH��![]() AB��1�����ù��ɶ�����ʽ���OD��Ȼ����������ε����߹�ϵ��֪��O��D��H���㹲��ʱ��DH�ij�����С��
AB��1�����ù��ɶ�����ʽ���OD��Ȼ����������ε����߹�ϵ��֪��O��D��H���㹲��ʱ��DH�ij�����С��
��1����ͼ1����AB��AC��AD��AC��
���Ե�AΪԲ�ģ���B��C��D���ڡ�A�ϣ�
�ߡ�BAC�ǡ�A��Բ�Ľǣ�����BDC��Բ�ܽǣ�
���BDC��![]() ��BAC��45�㣬
��BAC��45�㣬
�ʴ��ǣ�45��
��2����ͼ2��ȡBD���е�O������AO��CO��
�ߡ�BAD����BCD��90�㣬
���A��B��C��D��Բ��
���BDC����BAC��
�ߡ�BDC��25�㣬
���BAC��25�㣻
��3����������ABCD��AB��AD��CD����BAD����CDA����ADG����CDG��
�ڡ�ABE�͡�DCF�У�
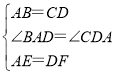 ��
��
���ABE�ա�DCF��SAS����
���1����2��
�ڡ�ADG�͡�CDG�У�
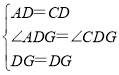 ��
��
���ADG�ա�CDG��SAS����
���2����3��
���1����3��
�ߡ�BAH����3����BAD��90�㣬
���1����BAH��90�㣬
���AHB��180��90�㣽90�㣬
ȡAB���е�O������OH��OD��
��OH��AO��![]() AB��1��
AB��1��
��Rt��AOD��OD��![]() ��
��
���������ε����߹�ϵ��OH��DH��OD��
�൱O��D��H���㹲��ʱ��DH�ij�����С��
��Сֵ��ODOH��![]() 1��
1��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����dzߣ���![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ����ͼ�ڷţ���
����ͼ�ڷţ���![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ������
������![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ�뷽����ת
˳ʱ�뷽����ת![]() ��
��![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��ֵΪ�� ��
��ֵΪ�� ��

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ö�������ͨ���ŷ����ƶ��ɵ����������Ƕ��������ز�֮һ����֪����ÿ���ɱ�10Ԫ.��������ÿ�������ۼ�![]() ��Ԫ������������
��Ԫ������������![]() ������֮��Ĺ�ϵ���±���
������֮��Ĺ�ϵ���±���
| 15 | 20 | 30 | �� |
| 25 | 20 | 10 | �� |
����������![]() �����ۼ�
�����ۼ�![]() ��һ�κ���������
��һ�κ���������
��1����������![]() �����������ۼ�
�����������ۼ�![]() ��Ԫ���ĺ�����ϵʽ.
��Ԫ���ĺ�����ϵʽ.
��2��Ҫʹ��������ÿ�����۵��������ÿ�������ۼ�Ӧ��Ϊ����Ԫ��ÿ�����۵���������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�з�ƶ���ھ���ƶ�����У���֯30������װ�˻��������ҡ�������������ۣ����ƻ�30������Ҫװ�ˣ�ÿ������ֻ��װ��ͬһ�ֲ�Ʒ���ұ���װ���������±��ṩ����Ϣ������������⣺
��Ʒ���� | ���� | ���� | ���� |
ÿ���������������֣� | 10 | 6 | 4 |
ÿ�����ز�������Ԫ�� | 0.7 | 0.8 | 0.5 |
��װ�˺��ҵ�����Ϊx����װ�˸����ij�������װ�˺��ҳ�������2����1������30����װ�˵����ֲ�Ʒ��������Ϊy��Ԫ��
(1)��y��x֮��ĺ�����ϵʽ��
(2)��װ����������������8���������������ʱ��װ�˸��ֲ�Ʒ�ij����������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ��������ÿ���ɱ�Ϊ50Ԫ�������ÿ��60Ԫ���ۣ�������800�������ÿ�����5Ԫ���ۣ����������ͼ���100��������̳�������������Ҫ������12000Ԫ����ʹ�˿ͻ�ø�����Żݣ���ô���ֳ����ۼ�Ӧ��Ϊ����Ԫ��
��1���������![]() Ԫ�������ֳ������ۼ�Ϊ___________Ԫ��������Ϊ____________��.
Ԫ�������ֳ������ۼ�Ϊ___________Ԫ��������Ϊ____________��.
��2���з�����ɱ���Ľ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
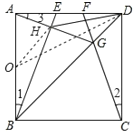
����Ŀ����ͼ��������![]() ����A����1��0����B��3��0�����㣬��y���ڵ�C����DΪ�����ߵĶ��㣬����BD����HΪBD���е㣮�����������⣺
����A����1��0����B��3��0�����㣬��y���ڵ�C����DΪ�����ߵĶ��㣬����BD����HΪBD���е㣮�����������⣺
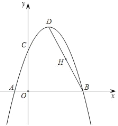
��1���������ߵĽ���ʽ������D�����ꣻ
��2����y������һ��P��ʹPD+PH��ֵ��С����PD+PH����СֵΪ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ء��㳡�衱�������ŵ����ⱶ�ܹ�ע�������Ա�Ա�����15~65������ε����������������飬��������������Ӧ��ͳ��ͼ������ԡ��㳡�衱�������ŵ�̬�����������֣�A��ûӰ�� B��Ӱ�첻�� C����Ӱ�죬�����������˶� D��Ӱ��ܴ���ȡ�� E���������������
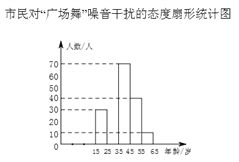
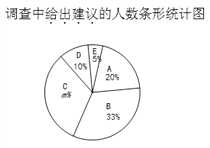
����������Ϣ����������⣺
��1������ͳ��ͼ��գ� ![]() ��A��������Ӧ������Բ�Ľ�Ϊ �ȣ�
��A��������Ӧ������Բ�Ľ�Ϊ �ȣ�
(2)�ڴ˴ε����У���������������⡱����25�ˣ�����һ�������˶����ˣ�
(3)������ͳ��ͼ����������
(4)�����ع���14���������ݴ˴ε��������Ʊ��������л��ж���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��![]() ����������ʾ�����˶���ÿ������������OABC�ı�ʱ����з���������ʱ����ǵ�������ǣ�����P��2018�����������εı�ʱ����P������Ϊ______��
����������ʾ�����˶���ÿ������������OABC�ı�ʱ����з���������ʱ����ǵ�������ǣ�����P��2018�����������εı�ʱ����P������Ϊ______��

���𰸡�![]()
��������
���ݷ����������ǵĶ�������ͼ�Σ���ͼ��֪��ÿ6�η���Ϊһ��ѭ��������ѭ������2018����6�������̺����������ȷ������Ӧ�ĵ�����꼴�ɣ�
�⣺��ͼ��ʾ������6�η�����ص�������![]() ��
��
![]() ��
��
![]() ����P��2018���������εı�ʱΪ��337��ѭ����ĵ�2�η�����
����P��2018���������εı�ʱΪ��337��ѭ����ĵ�2�η�����
![]() ��P������Ϊ
��P������Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
���㾦��
������Ҫ�����˵������Ĺ��ɣ�����ͼ�Σ��۲��ÿ6�η���Ϊһ��ѭ��������ѭ���ǽ���Ĺؼ���
�����͡������
��������
15
����Ŀ��Ϊ�˱���������ij������˾��������A��B�����ͺŵ�ȫ�»�϶�����������10��������A���ͺ�ÿ���۸�Ϊa��Ԫ��ÿ���ʡ����Ϊ![]() ������B���ͺ�ÿ���۸�Ϊb��Ԫ��ÿ���ʡ����Ϊ
������B���ͺ�ÿ���۸�Ϊb��Ԫ��ÿ���ʡ����Ϊ![]() �����������飬����һ��A�ͳ��ȹ���һ��B�ͳ���20��Ԫ������2��A�ͳ��ȹ���3��B�ͳ���60��Ԫ��
�����������飬����һ��A�ͳ��ȹ���һ��B�ͳ���20��Ԫ������2��A�ͳ��ȹ���3��B�ͳ���60��Ԫ��
![]() �����a��b��
�����a��b��
![]() ������������϶���������ÿ���ܽ�ʡ
������������϶���������ÿ���ܽ�ʡ![]() �������ͣ�����������϶�����������Ҫ������Ԫ��
�������ͣ�����������϶�����������Ҫ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
�����ӹ�ij�����Ͳ��ϣ�����Ҫ�����Ͻ��м��´�����ʹ���ֲ��ϱ�����һ�����¶ȷ�Χ�ڷ��ɽ��м����ӹ�![]() �������ֲ���ʱ�������¶�
�������ֲ���ʱ�������¶�![]() ��ʱ��
��ʱ��![]() �ĺ���
�ĺ���![]() ������С��ͬѧ�о��ú����Ĺ��̣���������������
������С��ͬѧ�о��ú����Ĺ��̣���������������
![]() �����������ϵ�У��Ա���x��ȡֵ��Χ��______��
�����������ϵ�У��Ա���x��ȡֵ��Χ��______��
![]() �����¼��17min��10��ʱ�������¶�y��ʱ��x�仯�������
�����¼��17min��10��ʱ�������¶�y��ʱ��x�仯�������
ʱ�� | 0 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
|
�¶� | 15 | 24 | 42 | 60 |
|
|
|
| m |
|
|
�ϱ���m��ֵΪ______��
![]() ��ͼ����ƽ��ֱ������ϵxOy�У��Ѿ�������ϱ��еIJ��ֵ�
��ͼ����ƽ��ֱ������ϵxOy�У��Ѿ�������ϱ��еIJ��ֵ�![]() ��������ĵ㣬�����ú�����ͼ��
��������ĵ㣬�����ú�����ͼ��
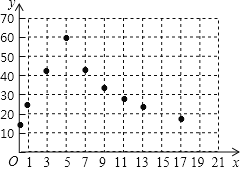
![]() �����г��ı���������ĺ���ͼ���Եõ�����
�����г��ı���������ĺ���ͼ���Եõ�����![]() ʱ��y��x֮��ĺ�������ʽΪ______����
ʱ��y��x֮��ĺ�������ʽΪ______����![]() ʱ��y��x֮��ĺ�������ʽΪ______��
ʱ��y��x֮��ĺ�������ʽΪ______��
![]() ���ݹ��յ�Ҫ�����ϵ��¶Ȳ�����
���ݹ��յ�Ҫ�����ϵ��¶Ȳ�����![]() ʱ�������Խ��в�Ʒ�ӹ�����ͼ����ʾ���¶ȱ仯�����У����Խ��мӹ���ʱ�䳤��Ϊ______min��
ʱ�������Խ��в�Ʒ�ӹ�����ͼ����ʾ���¶ȱ仯�����У����Խ��мӹ���ʱ�䳤��Ϊ______min��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com