
【题目】如图,抛物线![]() 经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
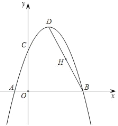
(1)求抛物线的解析式及顶点D的坐标;
(2)在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为
【答案】(1)![]() ,D(1,4);(2) PD+PH 最小值
,D(1,4);(2) PD+PH 最小值![]()
【解析】
(1)根据题意把已知两点的坐标代入,求出b、c的值,就可以确定抛物线的解析式,配方或用公式求出顶点坐标;
(2)由题意根据B、D两点的坐标确定中点H的坐标,作出H点关于y轴的对称点点H′,连接H′D与y轴交点即为P,求出H′D即可.
解:(1)∵抛物线![]() 过点A(-1,0),B(3,0),
过点A(-1,0),B(3,0),
∴![]() ,解得
,解得![]() ,
,
∴所求函数的解析式为:![]() ,
,
化为顶点式为:![]() =-(x-1)2+4,
=-(x-1)2+4,
∴顶点D(1,4);
(2)∵B(3,0),D(1,4),
∴中点H的坐标为(2,2)其关于y轴的对称点H′坐标为(-2,2),
连接H′D与y轴交于点P,

则PD+PH最小且最小值为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量![]() 与单价
与单价![]() 满足一次函数关系,求出
满足一次函数关系,求出![]() 与
与![]() 的关系式;
的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,可计算出甲的平均成绩是 环(直接写出结果);
(2)已知乙的平均成绩是9环,试计算其第二次测试成绩的环数;
(3)分别计算甲、乙六次测试成绩的方差,根据计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 箱中装有3张相同的卡片,它们分别写有数字1,2,4;
箱中装有3张相同的卡片,它们分别写有数字1,2,4;![]() 箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从
箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从![]() 箱、
箱、![]() 箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
(1)两张卡片上的数字恰好相同的概率.
(2)如果取出![]() 箱中卡片上的数字作为十位上的数字,取出
箱中卡片上的数字作为十位上的数字,取出![]() 箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(学习心得)于彤同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.例如:如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 外一点,且
外一点,且![]() ,求
,求![]() 的度数.若以点
的度数.若以点![]() 为圆心,
为圆心,![]() 为半径作辅助
为半径作辅助![]() ,则
,则![]() 、
、![]() 必在
必在![]() 上,
上,![]() 是
是![]() 的圆心角,而
的圆心角,而![]() 是圆周角,从而可容易得到
是圆周角,从而可容易得到![]() =________
=________![]() .
.
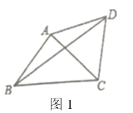
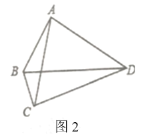
(2)(问题解决)如图2,在四边形![]() 中,
中,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
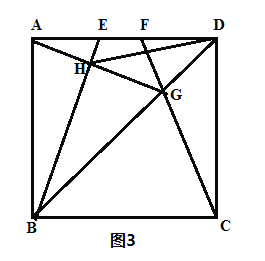
(3)(问题拓展)如图3,![]() 是正方形
是正方形![]() 的边
的边![]() 上两个动点,满足
上两个动点,满足![]() .连接交于点,连接
.连接交于点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交于点
交于点![]() ,若正方形的边长为2,则线段
,若正方形的边长为2,则线段![]() 长度的最小值是_______.
长度的最小值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
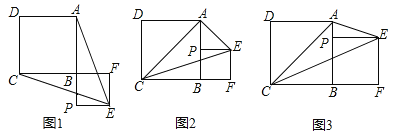
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标有的三个数值为﹣7,﹣1,3.乙袋中的三张卡片所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出卡片上的数值,把x、y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况.
(2)求点A落在第三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
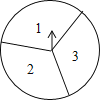
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 .
(2)小明和小颖用转盘做游戏,每人转动转盘一次,若两次指针所指数字之和为奇数,则小明胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或者列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
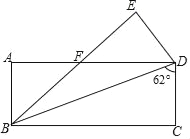
A. 31° B. 28° C. 62° D. 56°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com